24 см и 10 см.
Объяснение:
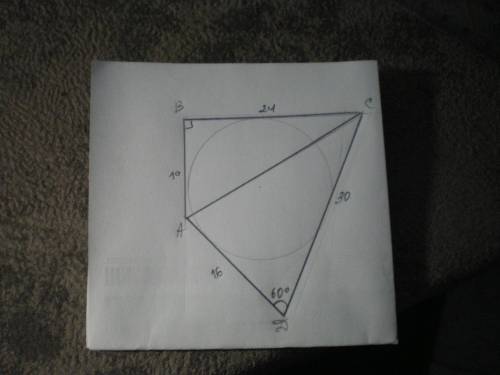
Если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны.
АВ+СD=АD+ВС
Проведем АС; ΔАВС - прямоугольный. Найдем АС из ΔАСD по теореме косинусов:
АС²=СD²+АD²-2*СD*АD*cos 60°=256+900-960*1/2=676;
АС=√676=26 см.
Если АВ+30=ВС+16, то ВС-АВ=14 см;
Пусть ВС=х см, тогда АВ=х-14 см.
По теореме Пифагора АС²=АВ²+ВС²; 676=(х-14)²+х²;
х²+х²-28х+196-676=0
2х²-28х-480=0
х²-14х-240=0
По теореме Виета
х=-10 (не подходит по условию) и х=24.
ВС=24 см; АВ=24-14=10 см.
Соединим точки A и D, D и C, С и B. Пусть AC∩BD=E.
∠ADB и ∠ACB вписанные и опирающиеся на хорду AB. Тогда они равны. Т.к. AB - диаметр, ∠ADB = ∠ACB = 90°.
Применив т. об отрезках пересекающихся хорд к хордам AC и DB, получим AE*EC=DE*EB.
Обозначим DE=a, EB=b, AE=c → с*EC=a*b → EC=a*b/c
AC ּ AE + BD ּ BE = (AE+EC)*AE+(BE+ED)*BE=c²+a*b+b²+a*b=c²+2ab+b²=(c²-a²)+(a+b)²=[по т. Пифагора для ΔADE (c²-a²)=AD². DB²=(DE+EB)²=(a+b)²]=AD²+DB²=[по т. Пифагора для ΔADB]=AB²
Т.к. AB - диаметр окружности, то значение AC ּ AE + BD ּ BE не зависит от положения точки E.
ответ: 36 см²
Объяснение:
Площадь трапеции найдём как сумму площадей четырёх треугольников, образованных диагоналями.
1. Рассмотрим ΔBOC и ΔCOD.
Проведём из точки C перпендикуляр CH к стороне BD. Получим, что CH является высотой и ΔBOC, и ΔCOD. Выпишем формулы площади для этих треугольников:
Найдём частное этих площадей:
2. ∠BCA = ∠CAD (накрест лежащие углы при BC || AD и секущей AC)
∠CBD = ∠BDA (накрест лежащие углы при BC || AD и секущей BD)
3. Рассмотрим ΔBOC и ΔAOD:
1) ∠BCA = ∠CAD
2) ∠CBD = ∠BDA
Следовательно, ΔBOC и ΔAOD подобны по двум углам.
Причём k = OC : OA = OB : OD = 1/2 ⇒ OA = 2OC
4. Рассмотрим ΔBOC и ΔAOD. Отношение площадей подобных треугольников равно квадрату коэффициенту подобия. То есть:
5. Рассмотрим ΔBOC и ΔABO.
Проведём из точки B перпендикуляр BK к стороне AC. Получим, что BK является высотой и ΔBOC, и ΔABO. Выпишем формулы площади для этих треугольников и преобразуем SΔABO:
6. Найдём площадь трапеции: