Треугольник с прямым углом - это прямоугольный треугольник.
Так как меньшие стороны "прилегают" к прямому углу, то эти стороны - катеты.
Так как катеты имеют длины 6 см и 8 см, то также такой треугольник - египетский (треугольник с соотношением сторон, равным 3:4:5). Следовательно, гипотенуза равна 10 см (можно также проверить через теорему Пифагора).
Высота, проведённая к большей стороне - высота, проведённая к гипотенузе (так как гипотенуза - самая большая сторона в прямоугольном треугольнике).
Высота, проведённая к гипотенузе равна произведению катетов, делённому на гипотенузу.
То есть -
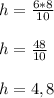
h = 4,8 см.
ответ: 4,8 см.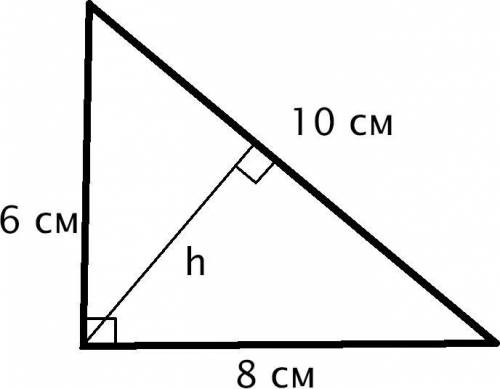
Доказать: КВ = ВМ; угол ВКМ = углу ВМК
Доказательство:
1.треугольник АВС - равнобедренный (АВ=ВС - дано)
треугольник ВАМ = треугольнику ВКС по первому признаку равенства треугольников (АВ=ВС - дано, АМ=КС - дано, угол ВАМ = углу ВСК), значит, все элементы треугольников равны => КВ=ВМ
2.угол 1 = углу 2 - доказано;
угол 1 + угол 3 = 180 градусов
угол 2 + угол 4 = 180 градусов
т.к. угол 1 = углу 2, угол 3= углу 4
(я знаю, доказательство 2 неточное; мысль есть - а сформулировать не получается)