Точка О - центр кола. ОВ, ОА - радіуси кола. Кут АОВ=40 градусів. Знайти два інші кути трикутника АОВ. - id1090619920210526 от vikakruchko1405 26.05.2021 17:48

Question

Геометрия: Точка О - центр кола. ОВ, ОА - радіуси кола. Кут АОВ=40 градусів. Знайти два інші кути трикутника АОВ. *

vikakruchko1405 · Accepted Answer

Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.

Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольников со стороной 3 см.

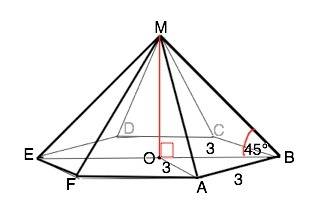
Обозначим пирамиду ABCDEF, центр - О.

Высота МО и половина ВО диагонали ВЕ образуют прямоугольный треугольник МОВ, острый угол МВО=45°. ⇒ Это равнобедренный треугольник, и МО=ВО=3 см.

Объём пирамиды равен 1/3 произведения высоты на площадь основания.

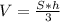
$V= \frac{S*h}{3}$

Площадь правильного шестиугольника – сумма площадей 6 правильных треугольников, площадь которых найдем по формуле:

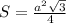
$S= \frac{ a^{2} \sqrt{3} }{4}$

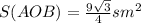
$S(AOB)= \frac{9 \sqrt{3} }{4}sm^{2}$

Площадь основания

6•9√3/4 sm²

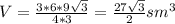
$V= \frac{3*6*9 \sqrt{3} }{4*3}= \frac{27 \sqrt{3} }{2}sm^{3}$

Сторона основание правильной шестиугольной пирамиды равна 3 см. боковое ребро составляет с плоскость

Точка О - центр кола. ОВ, ОА - радіуси кола. Кут АОВ=40 градусів. Знайти два інші кути трикутника АОВ. *

MOGZ ответил