ответ: 69
Объяснение:
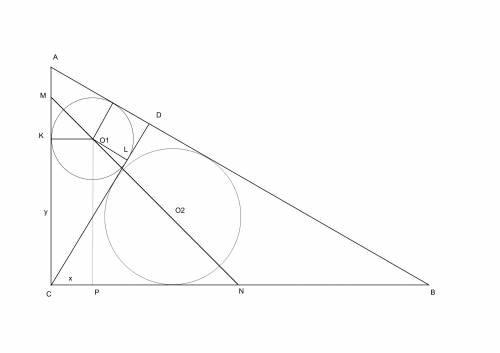
Если внимательно посмотреть на чертеж, то сразу видно, что CP + CK = CD; так как CP = KO1 = r = LD; CK = CL;
Обозначая CK = y; CP = x; CD = h (высота ABC), я получаю для точки O1
x + y = h;
Аналогично можно показать то же самое для центра второй окружности O2;
То есть если считать катеты осями прямоугольной системы координат, то уравнение прямой O1O2 так и будет x + y = h;
(прямая с таким уравнением проходит через эти две точки, а через две точки можно провести только одну прямую)
Это прямая, пересекающая оси под углом в 45 градусов, в точках (0, h) и (h, 0).
Отсюда следует, что треугольник CMN - равнобедренный, с катетами CM = CN = CD = h и площадью h^2/2;
Подставляя значения из условия, легко найти
h^2 = 18*2 = 36; h = 6;
Sabc = 23*6/2 = 69;
Формула через синус:
S = ab * sin(∠ab)/2
Синус через косинус:
sin(∠ab) = √(1 - (cos(∠ab))^2)
Теорема косинусов:
c^2 = a^2 + b^2 - 2ab * cos(∠ab)
c^2 - a^2 - b^2 = 2ab * cos(∠ab)
(c^2 - a^2 - b^2)/(2ab) = cos(∠ab)
Подставим найденный косинус во второе уравнение
sin(∠ab) = √(1 - ((c^2 - a^2 - b^2)/(2ab))^2)
Подставим наше уравнение в первое уравнение
S = ab * √(1 - ((c^2 - a^2 - b^2)/(2ab))^2) * 1/2
После того, как ты подставишь значения, получится 37/2 = 18,5
Я сделал проверку (по формуле Герона, конечно же) получился такой же ответ
P.s
Я прикрепил скрин из калькулятора
В первом уравнении я обозначил площадь за x, а во втором за S