ответ: Да, это параллелограмм.
Объяснение:
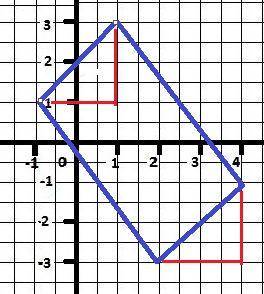
Рисунок задаче в приложении.
Составим уравнения прямых:
ДАНО: А(1;3), В(4;-1) НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(3-(-1))/(1-(4))= - 4/3 = -1,33 - коэффициент наклона прямой
2) b=Аy-k*Аx=3-(- 4/3)*1= 4 1/3- сдвиг по оси ОУ
Уравнение Y(АВ) = - 4/3*x+ 4 1/3
ДАНО: С(2;-3), D(-1;1) НАЙТИ: Y = k*x + b
1) k = ΔY/ΔX = (Сy-Dy)/(Сx-Dx)=(-3-(1))/(2-(-1))= - 4/3 - коэффициент наклона прямой
2) b=Сy-k*Сx=-3-(- 4/3)*2= - 1/3- сдвиг по оси ОУ
Уравнение Y(СD) = - 4/3*x - 1/3
Коэффициент наклона этих двух прямых одинаковый - параллельны.
И длина у них одинаковая - катеты у сторон одинаковый.
По условию задания составим уравнение расстояния произвольной точки М(х; у) от точки А(3; -4) в 3 раза большего, чем от точки М до прямой х = 5.
√((3 - x)² + (y - (-4))²) = |3*(5 - x)|.
Модуль в правой части взят, чтобы длина не была отрицательной для точек, расположенных правее линии х = 5.
Возведём обе части в квадрат.
9 - 6x + x² + y² + 8y + 16 = 9*(25 - 10x + x²).,
Приведём подобные: 8x² - 84x - y² - 8y + 200 = 0.
Выделим полные квадраты.
8(x² - 10,5x + 5,25²) - 8*5,25² - (y² + 8y + 16) - 16 + 200 = 0.
8(x - (21/4))² - (y + 4)² = (9/2).
Разделим обе части на (9/2).
((x - (21/4))²)/(9/16) - ((y + 4)²)/(9/2) = 1.
Получено искомое уравнение. Это уравнение гиперболы.
Центр её расположен в точке ((21/4); -4).
Полуоси: действительная равна а =√(9/16) = 3/4, мнимая b = 3/√2.
Найдем координаты ее фокусов: F1(-c;0) и F2(c;0), где c - половина расстояния между фокусами
Определим параметр c: c² = a² + b² = 9/16 + 9/2 = 81/16 .
c = 9/4.
Тогда эксцентриситет будет равен: е = с/а = (9/4)/(3/4) = 3.
Более детальное решение приведено во вложении. Там же дан график полученной линии.
ответ: 88 см²
Объяснение: 1) Проведём высоты трапеции ВМ и СК на основание АД. " Рассмотрим прямоугольные треугольники ΔАВМ и ΔСДК, у них АВ=СД (как боковые стороны), ∠А=∠Д (как углы при основании равноб. трапеции). Получим , что ΔАВМ = ΔСДК по гипотенузе и острому углу.⇒ АМ=ДК. 2 ) Из ΔАВМ имеем: АМ²= АВ² - ВМ² = 10² - 8² =36, ⇒ АМ=6 ⇒ДК=6. Поэтому АД= АМ+МК+ДК= 6+5+6= 17 (см). 3) Тогда площадь трапеции S =(АД+ВС)·ВМ/2= (17+5)·8/2= 22·4=88(см²)