Найти координаты и абсолютную величину вектора CM, если C(3;-5), M(7;5)

👇

Ответ:

dzhulijamalish

04.05.2023

Координаты: СМ(4;0) От вторых значений отнимаем первые
Величина: СМ= 4 см ( корень из суммы квадратов разницы двух координат)
Если что, спрашивайте в комментариях

4,6(4 оценок)

Открыть все ответы

Ответ:

MikassaSwag

04.05.2023

1)Пусть АВС-равнобедренный треугольник,АС-основание=12 см.

АВ=ВС=10 см

Проведем высоту ВН

Так как треугольник равнобедренный,то высота,проведенная к основанию,является и медианой,и биссектрисой.

Так как ВН-высота,то образуется прямоугольный треугольник АВН,причем из-за того,что ВН ещё и медиана,то АН=НС=12/2=6см.

Теперь по теореме Пифагора находим катет ВН

ВН=корень из(АВ^2-АН^2)

ВН=корень из(64)

ВН=8см

Sтреугольника АВС=(ВН*АС)/2

S=(8*12)/2

S=48 кв. см

ответ:48 кв.см.

2)параллелограмм ABCD

Проведём из угла В на AD высоту BK.

∆ABK-прямоугольный. ےА=30°

Следовательно BK=AB:2, как катет, лежащий против угла 30°

AB=12. Тогда BK=6; S=16×6=96 кв.см.

ответ:96 кв.см.

3)Дано:

АВСD-трапеция,

АВ=СD=13 см.

АD=20см

ВС=10см

Найти:S

Проводим высоту ВН,так как трапеция равнобедренная,то АН будет равен (20-10)/2=5 см

Образовался прямоугольный треугольник АВН,находим катет(высоту) ВН

ВН=корень из(АВ^2-AH^2)

ВН=корень из(169-25)

ВН=12 см.

S=((АD+ВС)/2)*ВН

S((20+10)/2)*12=180 кв.см.

ответ:180 кв.см

Подробнее - на -

Объяснение:

4,6(1 оценок)

Ответ:

софика4

04.05.2023

Радиусы вписанной в равнобедренный треугольник и описанной около равнобедренного треугольника окружности равны соответственно:

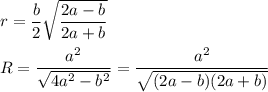$r = \dfrac{b}{2} \sqrt{ \dfrac{2a - b}{2a + b} } \\ \\ R = \dfrac{a^2}{ \sqrt{4a^2 - b^2} } = \dfrac{a^2}{ \sqrt{(2a - b)(2a + b)} }$ ,
где a - боковая сторона, b - основание, r - радиус вписанной окружности, R- радиус описанной окружности.

Сделаем замену переменных, чтобы было легче преобразовывать.
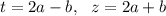
Пусть $t = 2a - b, \ \ z = 2a + b$

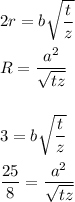
$2r = b \sqrt{\dfrac{t}{z} } \\ \\ R = \dfrac{a^2}{ \sqrt{tz} } \\ \\ \\ 3 = b \sqrt{\dfrac{t}{z} } \\ \\ \dfrac{25}{8} = \dfrac{a^2}{ \sqrt{tz} }$

Разделим первое уравнение на второе:

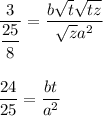
$\dfrac{3}{ \dfrac{25}{8} } = \dfrac{b \sqrt{t} \sqrt{tz} }{ \sqrt{z}a^2 } \\ \\ \\
 \dfrac{24}{25} = \dfrac{bt}{a^2} 
$

Сделаем обратную замену:

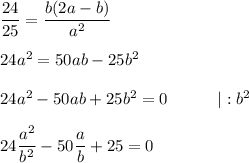
$\dfrac{24}{25} = \dfrac{b(2a - b)}{a^2} \\ \\ 
24a^2 = 50ab - 25b^2 \\ \\ 
24a^2 - 50ab + 25b^2 = 0 \ \ \ \ \ \ \ \ \ |: b^2 \\ \\ 
24 \dfrac{a^2}{b^2} - 50 \dfrac{a}{b} + 25 = 0$

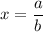
Пусть $x = \dfrac{a}{b}$

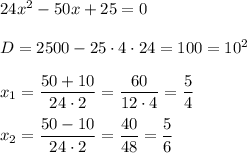
$24x^2 - 50x + 25 = 0 \\ \\ 
D = 2500 - 25 \cdot 4 \cdot 24 = 100 = 10^2 \\ \\ 
x_1 = \dfrac{50 + 10}{24 \cdot 2} = \dfrac{60}{12 \cdot 4} = \dfrac{5}{4} \\ \\ 
x_2 = \dfrac{50 - 10}{24 \cdot 2} = \dfrac{40}{48} = \dfrac{5}{6}$

Значит, боковая сторона относится к основанию как 5:4, либо как 5:6.

Обратная замена:

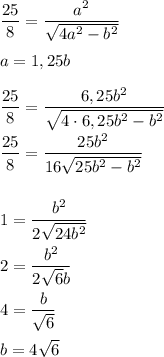
$\dfrac{25}{8} = \dfrac{a^2}{ \sqrt{4a^2 - b^2} } \\ \\ 
a = 1,25b \\ \\ 
 \dfrac{25}{8} = \dfrac{6,25b^2}{ \sqrt{4 \cdot 6,25b^2 - b^2 } } \\ \\ 
 \dfrac{25}{8} = \dfrac{25b^2}{16 \sqrt{25b^2 - b^2} } \\ \\ \\ 
1 = \dfrac{b^2}{2 \sqrt{24b^2} } \\ \\ 
2 = \dfrac{b^2}{2 \sqrt{6}b } \\ \\ 
4 = \dfrac{b}{ \sqrt{6} } \\ \\ 
b = 4 \sqrt{6}$

Получилось, что основание выражается иррациональным числом. Значит, данное значение не подходит.

Теперь решим второе уравнение:

$\dfrac{a}{b} = \dfrac{5}{6} \\ \\ 
\dfrac{25}{8} = \dfrac{a^2}{ \sqrt{4a^2 - b^2} } \\ \\ \\
 \dfrac{b}{a} = 1,2 \\ \\ 
\dfrac{25}{8} = \dfrac{a^2}{ \sqrt{4a^2 - b^2} } \\ \\ 
b = 1,2a \\ \\ 
 \dfrac{25}{8} = \dfrac{a^2}{ \sqrt{4a^2 - 1,44a^2} } \\ \\ 
\dfrac{25}{8} = \dfrac{a}{ \sqrt{2,56} } \\ \\ 
\dfrac{25}{8} = \dfrac{a}{1,6} \\ \\ 
a = 5 \\ \\ 
b = 1,2a = 6$

Значит, боковая сторона равна 5 см, а основание - 6 см.
ответ: 5 см; 5 см; 6 см.

4,7(26 оценок)

Это интересно:

Питомцы-и-животные

25.09.2021

Как безопасно подрезать крылья небольшой птице: Советы экспертов...

Дом-и-сад

17.04.2021

Волшебное искусство выращивания астр: секреты заботы, чтоб цветы радовали глаз долго...

Компьютеры-и-электроника

15.07.2020

Как правильно очистить экран iPhone и iPod Touch...

Стиль-и-уход-за-собой