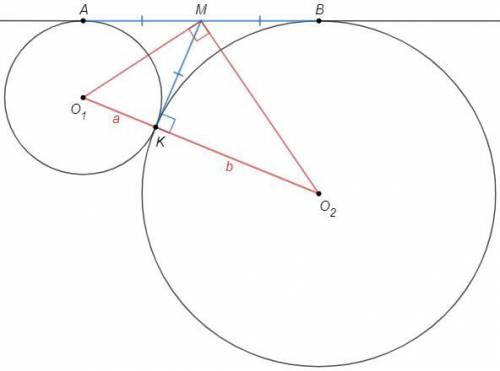
Рассмотрим две окружности, касающиеся внешним образом.
MK, AB - общие касательные
MA=MK=MB; MO1, MO2 - биссектрисы (т об отрезках касательных из одной точки)
∠O1MO2 =90 (биссектрисы смежных углов перпендикулярны)
∠MKO1 =90 (радиус в точку касания перпендикулярен касательной)
MK =√(O1K*O2K) =√(ab) (высота из прямого угла)
AB =2MK =2√(ab)
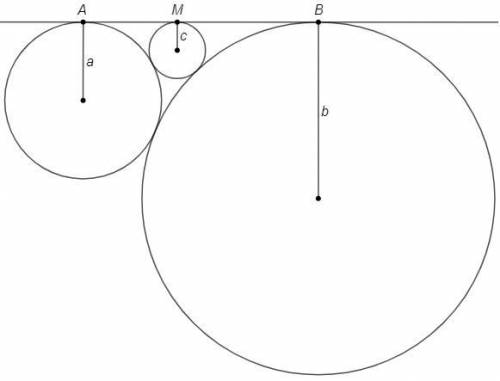
Теперь рассмотрим три окружности, для каждой пары выполняется предыдущее условие: касаются внешним образом и общей внешней касательной (c - меньший радиус).
AM =2√(ac)
BM =2√(bc)
AB =2√(ab) =AM+BM
=> √(ab) =√(ac) +√(bc) | :√(abc)
=> 1/√c = 1/√a + 1/√b
Два случая:
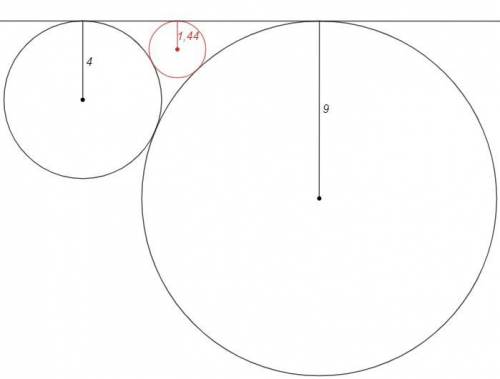
1) x - меньший радиус
1/√x =1/√4 +1/√9 => 1/√x =1/2 +1/3 =5/6 => x=36/25 =1,44
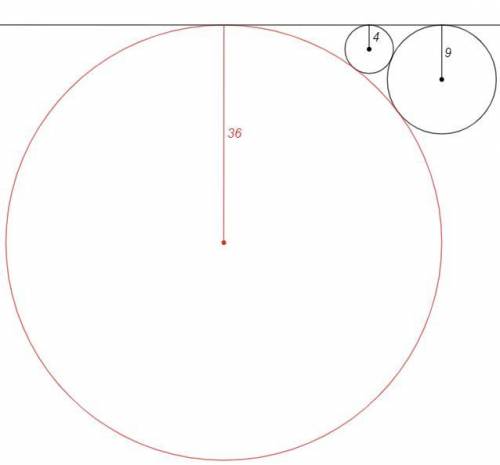
2) 4 - меньший радиус
1/√4 =1/√x +1/√9 => 1/√x =1/2 -1/3 =1/6 => x=36
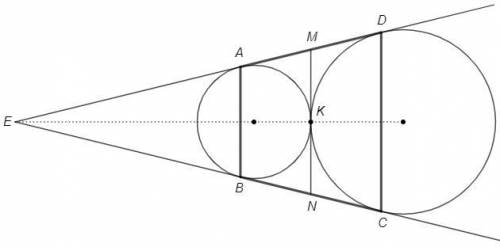
Пусть AD и BC пересекаются в точке E.
Отрезки касательных из одной точки равны, EA=EB, ED=EC.
△AEB, △DEC - равнобедренные => EAB =90 -E/2 =EDC => AB||DC
ABCD - трапеция
MA=MK=MD, NB=NK=NC (отрезки касательных из одной точки)
MN - средняя линия трапеции ABCD
MN =(AB+CD)/2 =(8+13)/2 =10,5
NB=NK=NC => NK=BC/2
Центры лежат на биссектрисе угла E (т.к. окружности вписаны в угол).
Точка внешнего касания окружностей K лежит на линии центров, то есть на биссектрисе угла E.
MN||AB => △MEN~△AEB =>
△MEN - равнобедренный, EK - биссектриса и медиана, NK=MN/2
BC =MN =10,5
LO/LT=3/5
Объяснение:
MNPQ-параллелограмм⇒MN║PQ, MQ║NP, ∠M=∠P
MK/PS = MT/PL, ∠M=∠P⇒ΔMKT~ΔPLS⇒∠PLS=∠MTK, ∠PSL=∠MKT, KT/LS=MK/PS = MT/PL=2/3
MN║PQ⇒∠MKS=∠PSK⇒
⇒∠TKO=∠MKS-∠MKT=∠PSK-∠PSL=∠LSO⇒∠TKO=∠LSO
∠KOT=∠SOL-вертикальные углы
∠TKO=∠LSO, ∠KOT=∠SOL⇒ΔKOT~ΔLOS⇒OT/LO=KT/LS=2/3
OT/OL=2/3
1+(OT/OL)=1+(2/3)
(OL+OT)/LO=5/3
LT/LO=5/3
LO/LT=3/5