Два круга имеют внутреннее прикосновение в точке А, причем меньше круг проходит через центр большей. Докажите, что любая хорда большей круги, которая выходит из точки А, делится меньшим кругом пополам.
Дано:окр С(R=CA) ,окр В (r=ВА) ,СА=2ВА, внутреннее касание в точке А.
Доказать :что любая хорда большего круга, выходящая из точки А, делится меньшей окружностью пополам.
Доказательство.
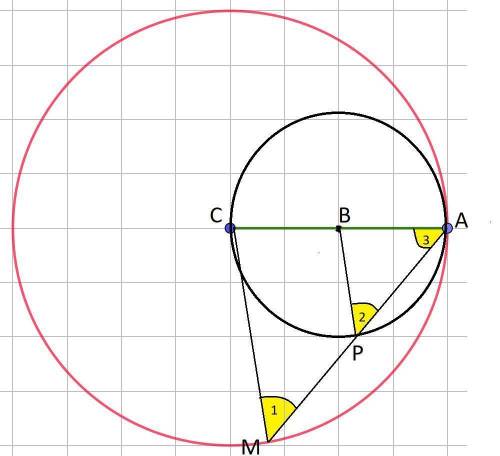
Пусть АМ-хорда большей окружности , пересекает меньшую окружность в точке Р. Необходимо доказать , что Р-середина АМ или АМ=2АР.
1)ΔАМС- равнобедренный , т.к СА=СМ=R, значит ∠1=∠3.
2) ΔАРВ-равнобедренный , т.к ВА=ВР=r, значит ∠2=∠3.
ΔАМС подобен ΔАРВ по двум углам : ∠1= ∠2 , ∠3-общий . В подобных треугольниках сходственные стороны пропорциональны :
СА:ВА=АМ:АР или 2ВА:ВА=АМ:АР или 2:1=АМ:АР , АМ=2АР , значит Р-середина.
Объяснение:
1) Пусть сторона основания равнобедренного треугольника равна х см, тогда боковые стороны равны (x+10) см. Зная, что периметр равнобедренного треугольника равен 98 см, составим уравнение
x + 2(x+10) = 98
x + 2x + 20 = 98
3x = 78
x = 26 см - сторона основания
Боковые стороны равнобедренного треугольника 26 + 10 = 36 см.
2) Теперь примем за х боковую сторону равнобедренного треугольника, тогда сторона основания равна (x+10) см. Составим уравнение
x + 10 + 2x = 98
3x = 88
x = 88/3 см - боковая сторона
88/3 + 10 = 118/3 см - сторона основания
Т.е. у обеих вариантов выполняется неравенство треугольника, значит данная задача имеет два решения.
ответ: 26 см, 36 см, 36 см или 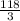 см,
см, 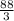 см,
см, 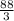 см.
см.
Объяснение:
Согласно следующему свойству:
Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.
AD : BD = AC : BC = 8 : 4 = 2 : 1
AD + BD = AB
Примем AD = 2x, BD = x
2x + x = 3x = AB = 6
x = 2, AD = 2x = 4
Треугольники BDE и BCA подобны(общий угол и равные углы BED и BAC за счет вписанного четырехугольника) с коэф. 2 (BС : BВ = 2 : 1), соответственно CA : DE = 2 : 1
DE = CA/2 = 8/2 = 4
DE = AD = 4