Построим прямоугольный треугольник с циркуля и линейки. Случай, когда данные стороны равны, рассматривать не будем, ибо в таком случае одна из них не может быть равна катету, а другая — гипотенузе.
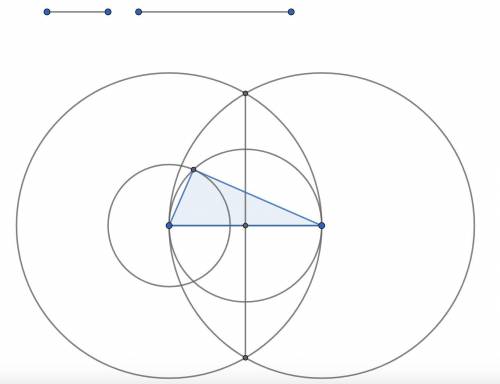
1. На большей стороне (гипотенузе, назовём её b) построим две окружности с центрами в концах отрезков и радиусом b. Проведём прямую через точки пересечения окружностей. Она будет пересекать гипотенузу в середине в силу симметричности чертежа.
2. Построим окружность с центром в середине гипотенузы и радиусом b / 2. Тогда эта окружность будет содержать концы отрезка, который будет являться для неё диаметром.
3. Построим окружность с центром в одном из концов гипотенузы (не теряя общности — в левом конце) и радиусом, равному меньшей стороне (катету, назовём его a). Отметим точку пересечения с окружностью, построенной в п. 2.
4. Проведём отрезок, соединяющий правый конец гипотенузы и точку пересечения окружностей (см. п. 3). Полученный треугольник (выделен на рисунке) будет прямоугольным, так как он вписан в окружность, один из его углов опирается на диаметр, то есть угол прямой.

Объяснение:
Пусть радиус основания цилиндра х, тогда высота цилиндра (х+12) см.
В осевом сечении цилиндра-прямоугольник⇒х(х+12)=90.
х²+12х-90=0 , Д=в²-4ас, Д=144+4*90=504=36*14
х₁=(-в+√Д):2а , х₁=(-12+6√14):2=-6+3√14=3√14-6>0 , т.к.3√14=√126, √126>√36.
х₂=(-в-√Д):2а , х₂=(-12-6√14):2.=-6-3√14 не подходит по смыслу задачи.
r=3√14-6 , h=12+3√14-6=6+3√14.
V=S(осн)*h.
S(осн)=Пr², S(осн)=П(3√14-6)²
V= П(3√14-6)² *(6+3√14)=П(3√14-6)² *(3√14+6)=П(3√14-6)*(3²√14²-6²)=
=П(3√14-6)*(126-36)=90П(3√14-6) (см²)