Вариант решения ( можно вычислять стороны, можно обойтись без вычислений )
ответ: tg∠АОВ=1
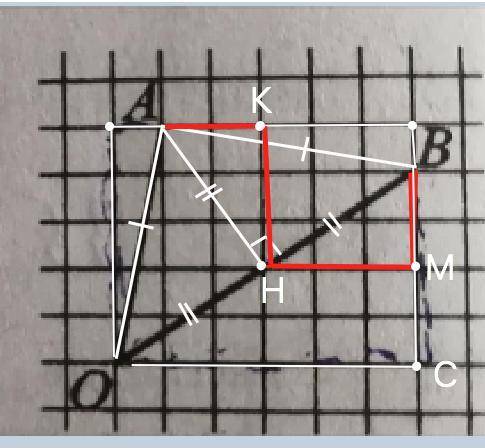
Объяснение: Соединим точки А и В. В получившемся треугольнике АОВ «пристроим» к сторонам АО и АВ прямоугольные треугольники. Они равны по двум катетам. Следовательно, АО=АВ, треугольник АОВ - равнобедренный.
К стороне ОВ "пристроим" прямоугольный треугольник. В ∆ ОВС МН - средняя линия. Н - середина ОВ. АН=ВН
Треугольники АКН и ВМН равны по двум катетам. => АН=ВН=ОН.
tg∠АОВ=1=АН:НО=1.
------------
Ясно, что все эти "пристроим" Не обязательно чертить, а сделать мысленно.
Продолжим сторону АС треугольника АВС за точки А и С ,
получим прямую ДЕ.
Проведём биссектрису АК угла ВАД, а также биссектрису СМ угла ВСЕ.
ВК⊥АК и ВМ⊥СМ
Продолжим высоты ВК и ВМ до пересечения с ДЕ. На ДЕ получим
точки Д и Е.
Так как АК и СМ - биссектрисы и высоты одновременно в ΔАВД и ΔВСЕ, то эти треугольники равнобедренные ⇒
АВ=АД и ВС=СЕ.
Высоты АК и СМ в равнобедренных треугольниках АВД и ВСЕ являются ещё и медианами , значит точка К - середина ВД, а точка М - середина ВЕ.
Рассм. ΔВЕД: КМ - средняя линия ΔВЕД.
ДЕ=ДА+АС+СЕ=АВ+АС+ВС=Р(АВС)=14 см
Средняя линия треугольника равна половине стороны, параллельно которой она проходит, то есть
КМ=1/2*ДЕ=1/2*14=7 см.