∆АВС – прямоугольный с прямым углом АВС по условию;
Сумма острых углов в прямоугольном треугольнике равна 90°, тогда угол АСВ=90°–угол ВАС=90°–45°=45°.
Получим что угол ВАС=угол АСВ, следовательно ∆АВС – равнобедренный с основанием АС.
Тогда АВ=ВС=100.
∆ABD – прямоугольный с прямым углом ABD по условию.
Сумма острых углов в прямоугольном треугольнике равна 90°, значит угол ADB=90°–угол BAD=90°–60°=30°.
В прямоугольном треугольнике против угла в 30° лежит катет, вдвое меньший гипотенузы.
Тоесть АВ=0,5*АD => АD=2*АВ=2*100=200.
По теореме Пифагора в прямоугольном ∆АВD:
AD²=AB²+BD²
200²=100²+BD²
40000–10000=BD²
BD=√30000
(BD=–√30000 не может быть, так как длина всегда положительна)
BD=100√3
CD=BD–ВС=100(√3)–100=100((√3)–1)
ответ: 100((√3)–1)
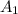, вторую 
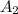, третью 
,
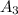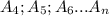соответственно . 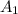к остальным вершинам соответственно , тогда из неравенство треугольников получим неравенства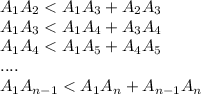 
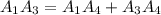(это означает что треугольник не вырожденный) и подставляя получим требуемое то есть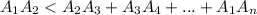 
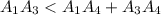
1. Медиана делит весь треугольник на 2 равной площади (высота общая, основания равны, поэтому равны площади).
2. Вторая медиана делит первую в отношении 1/2, то есть площади получающихся при этом треугольников относится так же. Имеется ввиду треугольник, отсеченный первой медианой, с вершиной, из которой выходит вторая медиана. Ясно, что высота у этих двух треугольнокв общая, поэтому площади относятся, как основания. То есть меньший будет иметь площадь 1/6 от всего тр-ка, а больший - 2/6.
3. Третья (:))) медиана разделит тот треугольник, который в 2 раза больше (из пункта 2.) на 2 треугольника - равной площади (см. пункт 1.). То есть каждый из них будет иметь площадь 1/6 от площади всего тр-ка.
4. Повторяя эти рассуждения для второго треугольника, отсеченного первой медианой, видим, что все треугольники имеют площадь 1/6 от площади всего тр-ка.