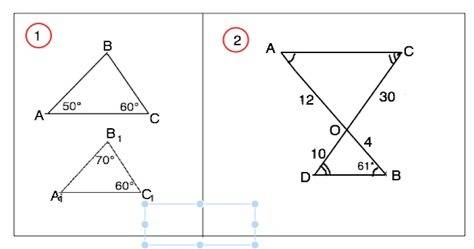
1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9
Объяснение:
8)
1)Т.к. EBC - прямой треугольник; угол BEC = 60 => угол EBC = 90 - 60 = 30; т.к. напротив угла в 30 лежит половина гипотенузы => EB = 2EC =
= 7*2 = 14
2)Т.к. углы AEB и BEC - смежные => угол AEB = 180 - 60 = 120 => угол ABE = 180 - 120 - 30 = 30 (Сумма углов в треугольнике) => треугольник ABE - равнобедренный => AE = BE = 14
3) Т.к. AE = 14; EC = 7 => AC = 14 + 7 = 21
9)
1) Т.к. AEO и DOC - прямые треугольники; EOA = DOC - вертикальные углы => углы EAO = OCD => EAO = DOC => треугольник AOC - равнобедренный
2) Т.к. угол OAC = углу OCA; угол EAO = углу DCO => угол BAC = углу BCA => треугольник ABC - равнобедренный => AB = BC
оценить и поставить сердечко, ибо не много дал за задание, да и времени потратил много.