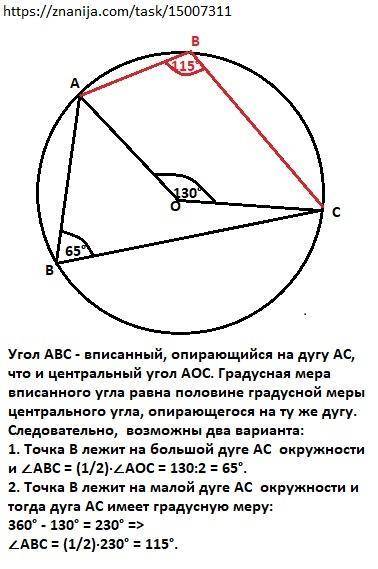
1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
ответ: 30°
Объяснение:
С циркуля замерим расстояние дуги, на которую опирается искомый вписанный угол , и сравним это расстояние с радиусом окружности.
Они получились одинаковые, но такое выполняется только для правильного шестиугольника ⇒ дуга, на которую опирается вписанный угол , равна 360°:6=60° и ∠α=30° по свойству вписанного угла.