Рѣшеніе:
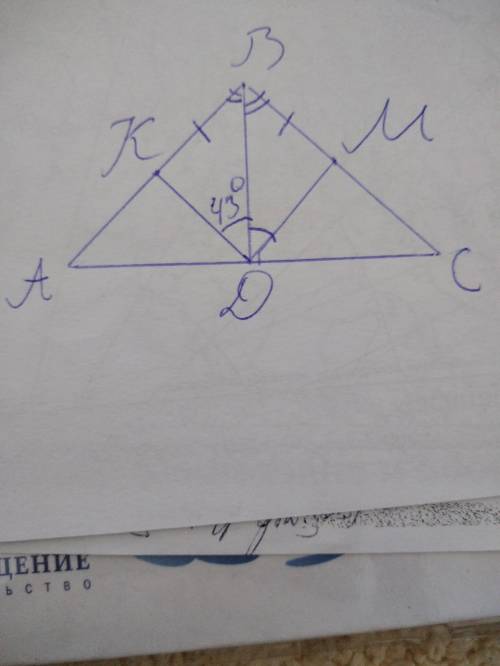
Рассмотрим треугольники КВD и BMD:
1). Сторона BD общая
2). Т.к. ВС=АС, а точки К и М делят их пополам, то ВК=ВМ.
3). ВD медиана, но в равнобедренных треугольниках медианы, проведённые к основанию являются и высотами и биссектрисами тоже. А значит ВD — биссектриса угла В, => углы МВD и KBD равны.
Из всего выше перечисленного следует, что треугольники KBD и BMD равны по 1 признаку равенства треугольников, значит все их элементы совпадают, значит угол КDB и MDB равны => угол МDB=43°
Отвѣтъ: угол МDB=43°.
Відповідь:
Пояснення:
по теоремі про три пенрпендикуляра( зворотня) :Якщо пряма, яка лежить у площині, перпендикулярна до проекції похилої на цю площину, то вона перпендикулярна і до самої похилої. І навпаки: якщо пряма, яка лежить у площині, перпендикулярна до похилої, то вона перпендикулярна і до самої проекції на цю площину.
ОС- це проекція ОЕ на площину АВСД, Так як ∠ЕОД=90°, то и ∠СОД=90° .
Так як ∠ЕОД=90, то діагоналі АС і ВД перпендикулярні. За властивістю диагоналей ромба: Якщо у паралелограма діагоналі перпендикулярні, то такий паралелограм – ромб.
Отже АВСД- ромб.
Так как треугольник ABC равнобедренный и его периметр равен 48, значит AB = BC, а AC = 48 - 2BC.
Высота BH делит AC пополам, соответственно, AH = HC = (48 - 2BC) / 2.
Площадь треугольника BHC равен 32 см.
Составляем уравнение:
BC + (48 - 2BC) / 2 + BH = 32;
Решаем уравнение:
2BC / 2 + (48 - 2BC) / 2 + BH = 32;
(2BC + 48 - 2BC) / 2 + BH = 32;
48 / 2+BH = 32;
24 + BH = 32;
BH = 32-24;
BH = 8
ответ: длина высоты BH равна 8 сантиметра.