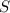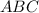
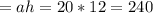△
см².
Пошаговое решение:
Дано:
△;
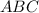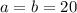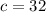см;
см;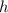
- высота;
Найти: △;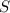
Решение:
Высота в равнобедренном треугольнике является одновременно и медианой, и биссектрисой. Медиана, проведённая из вершины угла в противоположную сторону, делит её на две равные части. Соответственно, проведённая из противоположного основанию угла высота делит его пополам. Перпендикуляр образует два прямоугольных треугольника. Боковая сторона 
равнобедренного треугольника представляет из себя гипотенузу. За катет берём получившуюся в результате раздела основания на две равные части сторону. По теореме Пифагора находим оставшийся катет, что и будет выступать в роли высоты.
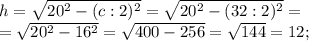
Находим площадь, умножив основание на высоту и поделив на 2.△
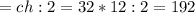(см²)
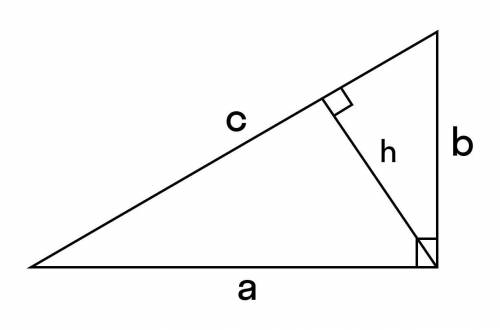
<ВАР=30⁰, <APB = 60⁰ в треугольнике АВР. Смежный угол <APC=120⁰
Треугольник АРС - равнобедренный (АР=РС по доказанному), РО - высота, медиана, биссектриса, т.е. <АРО=<СРО=60⁰, <РАО=30⁰ (сумма углов треугольника равна 180⁰)
<ВАД=90⁰, <ВАР=30⁰, <РАС=30⁰ <ОАТ=90-(30+30)=30⁰, значит <РАТ=60⁹
Получили, треугольник АРТ - равносторонний, т.к. <P=<A=<t=60⁰
Значит, РТ=АР=АТ=8см, Р(АРСТ)=8*4=32(см)
ответ:32см