Каждое ребро правильной шестиугольной призмы равно а. Найдите площадь поверхности призмы.
---
Призма называется правильной, если ее боковые ребра перпендикулярны основаниям, а основания – правильные многоугольники.
Все ребра правильной призмы равны, ⇒
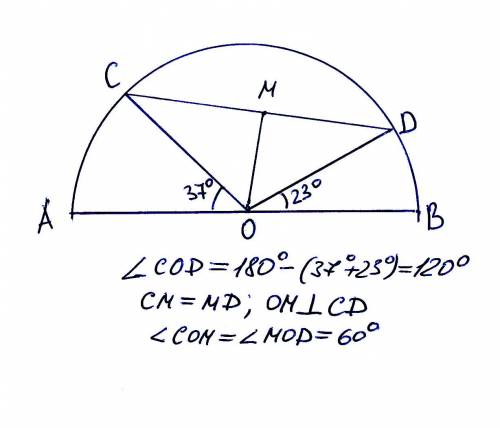
каждая из 6 боковых граней – квадрат, площадь которого S=a².
Ѕ(бок)=6а²
Основания правильной шестиугольной призмы - правильные шестиугольники, состоящие из 6 равных правильных треугольников.
Формула площади правильного треугольника S=(a²√3):4 ⇒
Ѕ (осн)•2=2•6•(a²√3):4=3а²√3
Площадь поверхности призмы равна сумме площадей: площади боковой поверхности и двух оснований.
S (призмы)= 6а²*+3•a²√3 или 3а²•(2+√3) ≈11,2а²
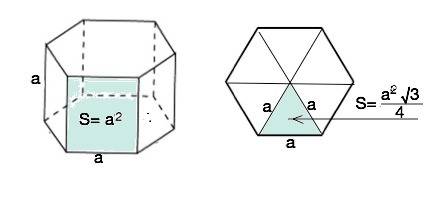
Главное, что нужно найти - это угол, стягиваемый хордой. То есть угол СОD.
Ясно, что
угол АОС + угол СOD + угол DOB = 180 градусов (полуокружность).
Поэтому
угол СOD = 180 - (23 + 37) = 120 градусов.
Построим РАВНОБЕДРЕННЫЙ треугольник COD и проведем в нем ОМ через середину CD. ОМ перпендикулярно CD, и ОМ делит угол COD пополам.
То есть треугольник СОМ прямоугольный, и угол СОМ = 60 градусов.
Поэтому ОМ = ОС/2 = R/2; (R - радиус окружности).
(если вам не понятно, откуда это взялось, то возьмите 2 треугольника СОМ и MOD и приставьте друг к другу не катетом ОМ, а катетами СМ = МD. Получится равносторонний треугольник, потому что все его углы будут 60 градусов. Значит ОМ = ОС/2)
Осталось вычислить СМ по теореме Пифагора, и умножить на 2, получим длину CD
СD = 2*корень(R^2 - (R/2)^2) = R*корень(3) = 15*корень(3).