Объяснение:
А1 1)8
d=2r=2*4=8
A2 3)3π
C=2πr=2π*1,5=3π
A3 3)75°
<вписанного=1/2 <центральный 150°:2=75°
A4 1)28 см
AB+CD=AD+BC
P=2(AB+CD)=2*14=28 см
A52)180°
В1
В окружность вписан квадрат со стороной;
Сторона квадрата а = 8 см;
Найдем длину дуги окружности, стягиваемой стороной квадрата.
1) Длина дуги находиться по формуле:
L = π * R * a/180°;
R = d/2;
d = диагональ квадрата.
2) Найдем диагональ квадрата по теореме Пифагора, если катеты равны стороне квадрата, то есть 8 см.
d = √(8^2 + 8^2) = √(64 + 64) = √(2 * 64) = 8√2 см;
С=πd= 8√2 π см
B2 1),2)3
B3
.Радиус ОА окружности является серединным перпендикуляром хорды СД,также с касательной ,проведенная через точку А,в точке касания образует прямой угол.Поэтому касательная ,проведенная через точку А, параллельна хорде СД.
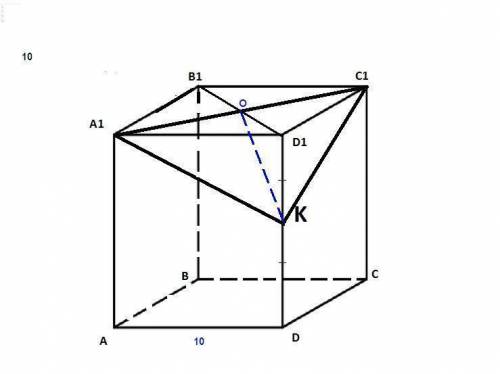
Соединяем точки А₁, С₁ и К, так как они попарно лежат в одной грани.
А₁С₁ = 10√2 как диагональ квадрата.
ΔА₁D₁K: по теореме Пифагора
А₁К = √(A₁D₁² + D₁K²) = √(10² + 5²) = √125 = 5√5
ΔA₁D₁K = ΔC₁D₁K по двум катетам (A₁D₁ = C₁D₁ как ребра куба, D₁K - общий), значит А₁К = С₁К = 5√5
Рa₁c₁k = 10√2 + 5√5 + 5√5 = 10√2 + 10√5 = 10(√2 + √5).
КО - медиана и высота равнобедренного треугольника А₁С₁К.
По теореме Пифагора:
КО = √(А₁К² - А₁О²) = √(125 - (5√2)²) = √(125 - 50) = √75 = 5√3
Sa₁c₁k = 1/2 · A₁C₁ ·KO = 1/2 · 10√2 · 5√3 = 25√6
Наклонная АВ, расстояние от наклонной к плоскости АС и проекция наклонной образуют прямоугольный треугольник АСВ, где ∠С = 90°.
Катет АС лежит напротив угла 30°, значит, он равен половине гипотенузы АВ.
Следовательно, гипотенузы АВ (наклонная):
АВ = 10² = 100 (см)
ответ: длина наклонной АВ = 100 см.