По рисунку определяем, что углы находим по функции arc tg по катетам.
Угол альфа = arc tg (3-1.5)/6 = arc tg(1/4).
Для элементов фурмы находим приращение высоты от 0 до 3-1,5 = 1,5.
Δ1 = 2*tgα = 2*(1/4) = 0,5.
Δ2 =4*tgα = 4*(1/4) = 1.
Δ3 = 6*tgα = 6*(1/4) = 1,5.
Высоты катетов:
h1 = 1,5+0.5 = 2 м.
h2 = 1,5+1 = 2,5 м.
h3 = 1,5+1.5 = 3 м.
Приводим значения углов:
α β γ θ
0,25 1 1,25 1,5 тангенс угла
0,24498 0,7854 0,8961 0,9828 радиан
14,0362 45 51,340 56,3099 градусов.
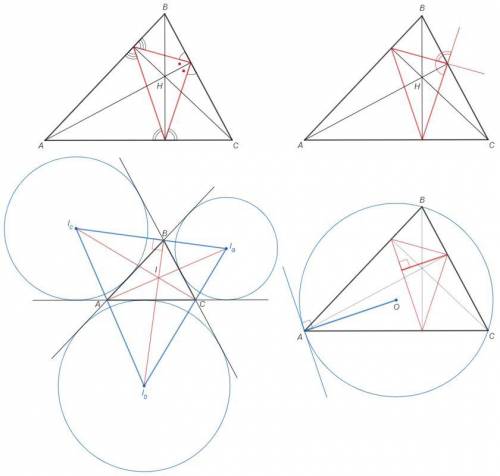
биссектриса ортотреугольника является высотой исходного треугольника
ДА. Стороны ортотреугольника образуют со стороной BC равные углы. Вычитая из прямых углов, получаем равные углы.
биссектриса внешнего угла ортотреугольника является стороной исходного треугольника
ДА. Биссектриса ортотреугольника является высотой ABC. Биссектрисы смежных углов перпендикулярны, следовательно сторона BC - внешняя биссектриса ортотреугольника.
I — ортоцентр треугольника IaIbIc
ДА. Биссектрисы внешнего и внутреннего углов перпендикулярны. Для треугольника IaIbIc треугольник ABC является ортотреугольником.
высота ортотреугольника параллельна радиусу описанной окружности, проведённому в соответствующую вершину
ДА. Сторона ортотреугольника антипараллельна стороне BC. Касательная через вершину A антипараллельна стороне BC. Сторона ортотреугольника и касательная параллельны. Тогда перпендикуляры к ним - высота ортотреугольника и радиус в точку касания - также параллельны.
----------------------------------------
высота ортотреугольника является биссектрисой исходного треугольника
НЕТ. Высота ABC является биссектрисой ортотреугольника.
H — центр описанной окружности треугольника IaIbIc
НЕТ. Центр описанной окружности IaIbIc симметричен I относительно O.
биссектриса ортотреугольника параллельна радиусу описанной окружности, проведённому в соответствующую вершину
НЕТ. Биссектриса ортотреугольника параллельна радиусу вписанной окружности.
Фото
Объяснение: