1) Как называется утверждение которое нельзя доказать?
Аксиома.
2) Из теоремы "Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны" составьте обратную.
Меняем "если" и "то" местами: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
3) Как называются прямые на плоскости, не имеющие общих точек?
Параллельными.
4) Если прямая a параллельна прямой b, и прямая а параллельна прямой с, то что можно сказать о прямых b и c?
Тогда b║c.
5) Изобразите: две параллельные прямые пересеченные секущей, отметьте числами 5 и 6 углы, которые являются односторонними.
См. рисунок.
6) О равенстве каких углов можно утверждать, если параллельные прямые пересечены секущей.
Тогда равны накрест лежащие углы: ∠1 = ∠7, ∠4 = ∠6
и равны соответственные углы: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, ∠4 = ∠8.
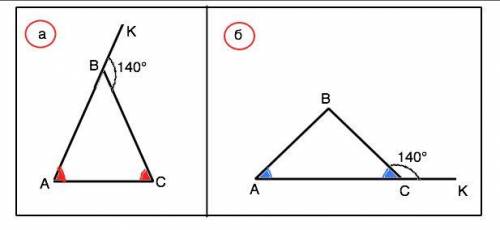
ответ: а) 40°, 70°, 70°. б) 40°, 40°, 100°.
Задача имеет два решения.
а) Дан внешний угол при вершине В, противолежащей осноанию. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
По условию ∆ АВС - равнобедренный. Поэтому ∠А=∠С=140°:2=70°.
б) Данный внешний угол - смежный с одним из внутренних углов при основании треугольника АВС. Развернутый угол АСК равен сумме смежных углов = 180°. ⇒ угол ВСМ=180°-140°=40°
∠ВАС=∠ВСМ=40°
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним. Угол ВАС+СВА=140° ⇒ ∠АВС=140°=40°=100°
можно взять любую призму..возьмем четырехугольную, прямую призму..
боковое ребро оно же и высота.. = 7..диагональ призмы равна 14.
получается прямоугольный треугольник с катетом 7 и гипотенузой 14
отметим угол между этой диагональю и основанием А.
тогда SinA = противолежащий катет деленный на гипотенузу.(катет 7 лежит напротив угла А) = 7/14 = 1/2
SinA = 1/2 = 30 градусов.