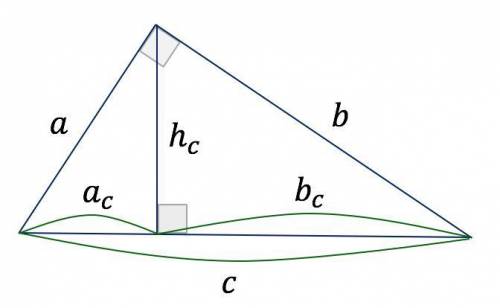
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою 
і проекцією цього катета на гіпотенузу:
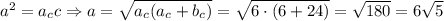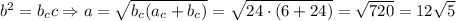см
см
Площа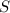 
прямокутного трикутника знаходится як півдобуток його катетів:
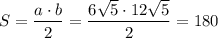см²
Другий б
Висота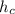 
прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
см
Площа 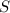будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти 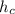, що до неї проведена:
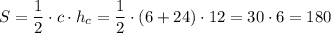см²
Відповідь: 180 см².
ответ:Если две прямые на плоскости,в данный момент это ВК и MN ,перпендикулярны к одной и той же прямой АС,то они параллельны,т к к прямой в плоскости из любой точки можно провести только один перпендикуляр
Параллельность прямых доказана
Теперь об углах
<СМN и <СВК являются соответственными и равны между собой
<СМN=<CBK=46 градусов
В условии сказано,что ВК биссектриса угла АВС
Биссектриса делит угол из которого она проведена на два равных угла,один из них угол СВК
<АВС=<СВК•2=46•2=92 градуса
Объяснение: