Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Объяснение:
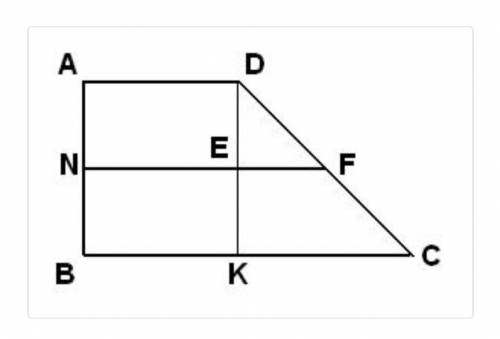
DK – перпендикуляр к ВС (см.рисунок). Так как NF - средняя линия трапеции, то AN = NB = DE = EK = AB/2 = 12/2 = 6 cм. Поскольку угол BCD = 45 градусов, то и угол NFD = 45. Тогда DE = EF = 6 см. Следовательно NE = BK = AD = NF – EF = 20 – 6 = 14 cм. В треугольнике DKC EF – его средняя линия. Посему KC = 2EF = 2*6 = 12 см. Таким образом ВС = ВК + КС. Но выше было найдено, что ВК = NE = AD = 14 см. Тогда ВС = 14 + 12 = 26 см. ВС можно было бы найти и иначе. Помните? Средняя линия трапеции равна полусумме оснований. Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм
Объяснение:
DK – перпендикуляр к ВС (см.рисунок). Так как NF - средняя линия трапеции, то AN = NB = DE = EK = AB/2 = 12/2 = 6 cм. Поскольку угол BCD = 45 градусов, то и угол NFD = 45. Тогда DE = EF = 6 см. Следовательно NE = BK = AD = NF – EF = 20 – 6 = 14 cм. В треугольнике DKC EF – его средняя линия. Посему KC = 2EF = 2*6 = 12 см. Таким образом ВС = ВК + КС. Но выше было найдено, что ВК = NE = AD = 14 см. Тогда ВС = 14 + 12 = 26 см. ВС можно было бы найти и иначе. Помните? Средняя линия трапеции равна полусумме оснований. Следовательно ВС = 2NF – AD = 2*20 – 14 = 40 -14 = 26 cм

Если катеты равны AB=6 и BC=8, то гипотенуза АС = 10.
Так как боковые ребра равны 13, то вершина пирамиды проецируется в середину гипотенузы.
Поместим пирамиду в систему координат: В - начало, ВА по оси Ох, ВС по оси Оу.
Середина ВС это точка К, середина АД - точка М.
Высота Н пирамиды равна:
Н = √13² - 5²) = √(169 - 25) = 12.
Находим координаты концов заданных отрезков.
К(0; 4; 0), М(4,5; 2;6).
С(0; 8; 0), Д(3;4; 12).
Векторы: CD = √((xD-xC)²+(yD-yC)²+(zD-zC)²) = 3 -4 12 169 13
KM = √((xM-xK)²+(yM-yK)²+(zM-zK)²) = 4,5 -2 6 60,25 7,762087348 .
Скалярное произведение векторов равно:
13,5 8 72 Скал_про = 93,5
cos α = 93,5/(13*√60.25) = 0,9266 .
Угол равен 0,3855 радиан или 22,09 градусов.