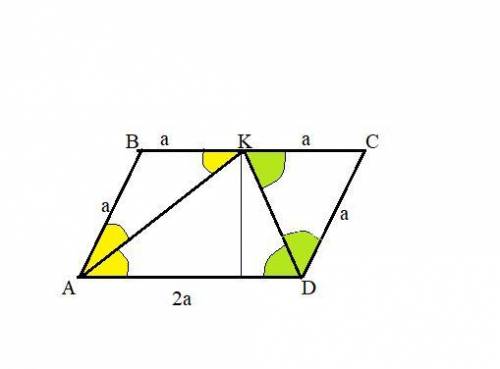
В параллелограмме ABCD биссектрисы углов A и D пересекаются в точке К,которая принадлежит стороне ВС.Найти площадь параллелограмма,если площадь треугольника AKD = 15 см^2.
Объяснение:
Пусть АВ=DС=а.
По свойству накрест лежащих углов при АD║BC и
-секущей АК ⇒∠DAK=∠AKB ⇒ΔABK равнобедренный и АВ=ВК=а ;
-секущей DК⇒∠АDK=∠СКD ⇒ΔDKС равнобедренный и DС =СК=а.
Значит AD=BC=2a
S(AKD)=0,5*AD*h=0,5*2а*h=a*h
S(ABK)+S(DCK)=0,5*ВК*h+0,5*КС*h=0,5h(BK+KC)=0,5h*2a=a*h ⇒
S(AKD)=S(ABK)+S(DCK)=15 (см²)
S( паралл)=S(AKD)+S(ABK)+S(DCK)=15+15=30 (см²)
1) 8 2) 8
Объяснение:
Прости, без синусов и косинусов не получится, но вот решение
В треугольнике ABC <А=15, <B=75, значит <С=180-15-75=90
Треугольник ABC - прямоугольный и АВ - гипотенуза
Формула длины высоты через гипотенузу и острые углы:
Н=с*sin α*cos α=AB*sin 15*cos 15
AB=H : sin 15*cos 15=2 : sin 15*cos 15=2 : (1/2*sin 30)=4 : 1/2=8.
А вот тут получется без sin и cos.
Для начала, нужно построить рисунок, после построения мы видим, что DH=2, и он лежит против угла DBH, который равен 30 градусам, значит BH=4. ВН лежит против угла С, который равен 30 градусам, значит ВС равен 8.
ответ: 8
Объяснение:
1) и а) и б) будут 8,5 т.к вписанный угор равен половине соответствующего
2)20:4=5 одна сторона
s=5*5=25
3) 180-10-(180-40)= 170-140=30°
4) не знаю;(