Расстояние от точки до прямой измеряется длиной отрезка, проведенного перпендикулярно этой прямой.
Обозначим угол АОВ, заданный отрезок – КМ. Любая точка, лежащая на биссектрисе угла, равноудалена от сторон этого угла.(свойство биссектрисы)
Следовательно, точка, равноудаленная от сторон угла АОВ, лежит на его биссектрисе.
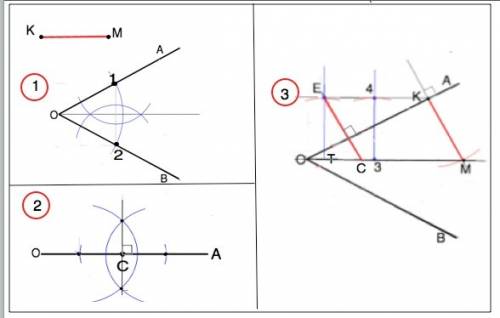
1. Построение биссектрисы (рис.1 приложения).
Из т. О как из центра произвольным раствором циркуля отметим на сторонах угла точки 1 и 2. Из этих точек раствором циркуля взятым так, чтобы он был больше половины расстояния между точками 1 и 2, проведем полуокружности до их пересечения двух точках. Точки пересечения и вершину угла соединим. Биссектриса построена.
2. Из произвольной точки С на биссектрисе проведем к стороне ОА перпендикуляр и отметим на нем отрезок СЕ, равный заданному отрезку КМ. ( как это делать - Вы наверняка знаете. см. рис. 2)
3. Из т.Е проведем прямую параллельно биссектрисе.
Для этого из т. Е опустим на прямую, содержащую биссектрису, перпендикуляр ЕТ. Из произвольной точки 3 возведем второй перпендикуляр и отложим на нем отрезок, равный отрезку ТЕ в т.4. Проведем через Е и т.4 прямую до пересечения со стороной угла АОВ в т.К.
4. Из т.К проведем перпендикуляр к стороне ОА. Он пересечется с биссектрисой в т.М, параллелен ЕС, его длина равна длине заданного отрезка (свойство параллельных прямых, пересекающих другие параллельные прямые). .
Точка М - искомая, расстояние от нее до другой стороны угла по свойству биссектрисы равно КМ.
Объяснение:
ΔАВС, ∠С=90°
Пусть точки касания лежат так С-Р-А , С-М-В , А-К-В.
По свойству отрезков касательных :
АК=АР=m=4 см,
ВК=ВМ=n=6см,
Радиус, проведенной в точку касания , перпендикулярен касательной⇒СРОМ-квадрат и СР=СМ=r=2 см.
Р(АВС)=АВ+ВС+СА=(4+6)+(6+2)+(2+4)=24(см)