я точно знаю, что раньше скалярным произведением называлась сумма произведений соответствующих координат, к примеру, вектор а с координатами х₁ и у₁, вектор b имеет координаты х₂;у₂
тогда скалярное произведение а*b= х₁*у₁+х₂*у₂
совсем недавно столкнулся с тем, что теперь это трактуют как теорему, а определяют скалярное произведение как произведение длин векторов на косинус угла между ними.
т.е. а*b=IаI*IbI*cosβ
По скалярному произведению можно определить вид угла. Если скалярное произведение двух ненулевых векторов равно нулю, то угол между векторами прямой. Если скалярное произведение двух ненулевых векторов больше нуля, то угол между векторами острый, а скалярное произведение меньше нуля, то угол тупой. Справедливы и обратные утверждения. т.е. если угол прямой, тупой, острый, то скалярное произведение соответственно равно нулю, меньше или больше нуля.
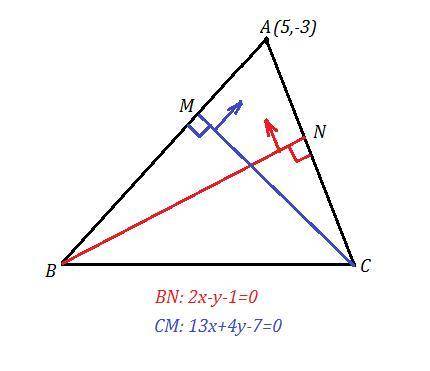
Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.
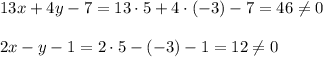
Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.
BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN:  .
.
Точка А(5,-3)∈АС и уравнение АС имеет вид:
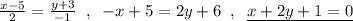
CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ:  .
.
Точка А(5,-3)∈АВ и уравнение АВ имеет вид:
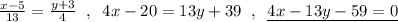
Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .
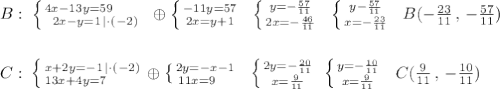
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:
a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.