1 вариант с чертежами Дуга АВ равна 126 градусов. Найдите величину центрального и вписанного угла, опирающегося на данную окружность.
2.Величина вписанного угла АВС равна 65 градусов. Найдите величину угла АДС, опирающегося на данную окружность.
3.Вписанный угол АВС опирается на полуокружность. Угол С равен 54 градуса. Найдите угол А.
4.Хорды АВ и СД пересекаются в точке М. АМ=5см, МВ=4см, СМ=10см. Найдите отрезок МД
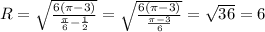
Поэтому задача может быть решена только в общем виде.
Площадь сектора:
Sсект = πR²α / 360°
Если угол задан в радианах, то
Sсект = πR²α / (2π) = 1/2 · R²α
Площадь треугольника АВС:
Sabc = 1/2 · R²·sinα
Площадь сегмента:
Sсегм = Sсект - SΔabc = 1/2 · R²α - 1/2 · R²·sinα = 1/2 · R²(α - sinα)
По условию, площадь сегмента равна 3π - 9:
1/2 · R²(α - sinα) = 3π - 9
R² = (6π - 18) / (α - sinα)
R = √( (6π - 18) / (α - sinα) )
По этой формуле можно вычислить радиус, если известен угол сектора.
Например:
α = π/6