Задача 1. В равнобедренном треугольнике АВС боковая сторона АС равна 5см, D- точка пересечения медиан АА1 и СС1. Отрезок DC1 равен 4/3см. Найдите площадь треугольника АВС.
Задача 2. В равностороннем треугольнике МНК биссектрисы пересекаются в точке О. Расстояние от точки О до стороны МН равно 6см. Найдите площадь треугольника НОК.
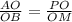
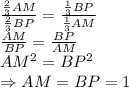
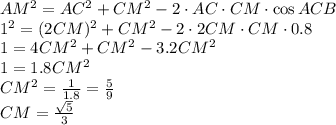
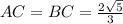
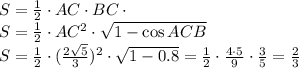
для нахождения радиуса строим два прямоугольных треугольника. первый: rcd и второй rbd
нам известно, что отрезок ac=20см, bc=12см, dc=17см.
так как rc=rb+bc; rb=ab/2; ab=ac-bc, получаем rc=(ac-bc)/2+bc=(20-12)/2+12=16см
по теореме пифагора находим катет rd=
применяем вновь теорему пифагора, для того чтобы найти гипотенузу db в треугольнике rbd
rb=ab/2; ab=ac-bc, получаем rb=(ac-bc)/2=(20-12)/2=4см
гипотенузу db так же является искомым радиусом окружности.
ответ: r=7см