68. По данным на рисунке найдите площадь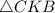 
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :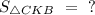
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,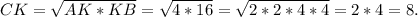 
Следовательно,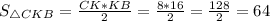 
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите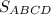 
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :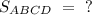
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,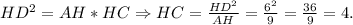 
Следовательно,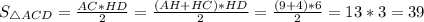 
ед².
Тогда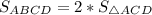 
= 2*39 ед² = 78 ед².
78 ед².
Начну с задачи №2(она полегче)
Итак,чтобы решить эту задачу нам достаточно знать соотношение R/(H-R)=r/√H²-r²
Найдем H в треугольнике конуса:
H²=10²-6²
H=8см
Знаем,что r=6см
Можем находить радиус шара по формуле выше.
Когда подставим получаем,что:
6(8-R)=10R
48=16R
R=3см
Vшара=4*П*R³/3
Vшара=4*27П/3=36П см³
ответ:36см³
Задача №1
Vконуса=Sосн*H/3
Итак, tgα=r/h (из прямоугольного треугольника конуса)
r=tgα*H
Проведем из центра шара отрезок в любую вершину при основании, и видим:
(H-R)²=R²-tg²α*H²
H=2R/(1+tg²α)
Sосн=П*r²=П*tg²α*H²=П*tg²α*4R²/(1+tg²α)²
Vконуса=Sосн*H/3=2*П*tg²α*R³ /(1+tg²α)³
ответ: 2*П*tg²α*R³ /(1+tg²α)³