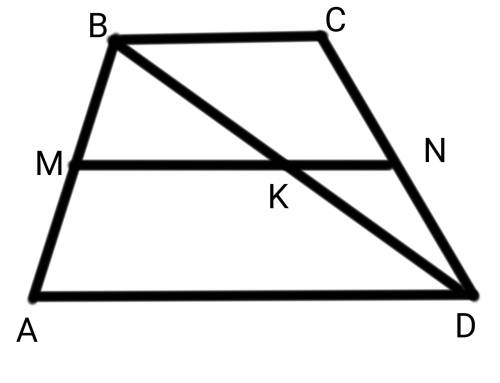
AD=20, BC=6, BM=AM, CN=ND.
Теорема Фалеса гласит, что если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
То есть, так как CN=ND и BC||KN, отрезки BK и KD равны.
Следовательно KN средняя линия треугольника BCD. А средняя линия треугольника равна половине параллельной стороны. Параллельная сторона KN это BC. BC=6, поэтому KN=6/2=3. Меньший отрезок равен 3.
По тем же свойствам, что и сверху MK средняя линия треугольника ABD и равна половине AD. AD=20.
MK=20/2=10
Больший отрезок равен 10
Объяснение:
без рисунка. на уровне формул. что дает условие " Боковое ребро этой пирамиды наклонено к плоскости основания под углом 45"? То, что радиус основания - радиус описанной около равностороннего треугольника окружности - равен высоте пирамиды. (она совпадает здесь с высотой конуса) R=H.
Площадь основания, если принять за а - сторону основания, равна S=а²√3/4, и а₃ =R√3, ⇒S=3R²√3/4=3√3R²/4
объем пирамиды равен v=(1/3)*sосн.*H
подставляем все выраженное через радиус основания конуса в объем пирамиды, т.е.
(1/3)*(3√3R²/4)*R=432⇒R=∛(432*4/√3)=∛(432*4*√3/3)=∛(16*27*4√3/3)=
4*3∛(√1/3)=12 ∛(√1/3)можно. конечно. дать ответ без иррациональности. и даже с корнем шестой степени , я оставлю. как есть.