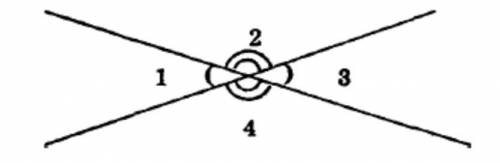
Объяснение:
1)
<1+<3=120° по условию.
<1=<3 вертикальные углы.
<1=120°:2=60°
<1+<2=180°, смежные углы их сумма равна 180°
<2=180°-<1=180°-60°=120°
<2=<4, вертикальные углы.
ответ: <1=60°; <2=120°; <3=60°; <4=120°
2)
<2-<1=20° по условию.
<2+<1=180° смежные углы
Пусть градусная мера угла <2 будет х°; тогда градусная мера <1 будет у°. Разность этих углов
х-у=20°.
Сумма этих углов
х+у=180°
Составляем систему уравнений
{х-у=20
{х+у=180
Метод алгебраического сложения
2х=200
х=200/2
х=100° градусная мера угла <2
Подставляем значение х в одно из уравнений
х+у=180
100+у=180
у=180-100
у=80° градусная мера угла<1.
<1=<3, вертикальные углы
<2=<4 вертикальные углы.
ответ: <1=80°; <2=100°; <3=80°; <4=100°
после построения mn получается треугольник mne, подобный треугольнику cde по первому признаку подобия (угол е - общий, углы с и nme равны как соответственные углы при пересечении двух параллельных прямых cd и mn секущей се). поскольку треугольники подобны, то
< mne = < cde = 68°
зная, что развернутый угол равен 180°, находим угол dnm:
< dnm = 180 - < mne = 180 - 68 = 112°
поскольку dm - биссектриса, то угол mdn = < cde : 2 = 68 : 2 = 34°
зная два угла треугольника dmn, находим неизвестный угол:
< dmn = 180 - < mdn - < dnm = 180 - 34 - 112 = 34°