1) S = 121,5·π см². 2) S = 16√15 см². 3) R = 10√3/3 см.
Объяснение:
1) Площадь осевого сечения - площадь квадрата, так как D = L.
D² = 81 см². => D = L = 9 см.
Площадь полной поверхности цилиндра равна
2·So + Sбок = 2·π·(D/2)² + 2·π·(D/2)·L.
В нашем случае
S = 2·π·(D/2)·(D/2+L) = π·9·13,5 = 121,5π см².
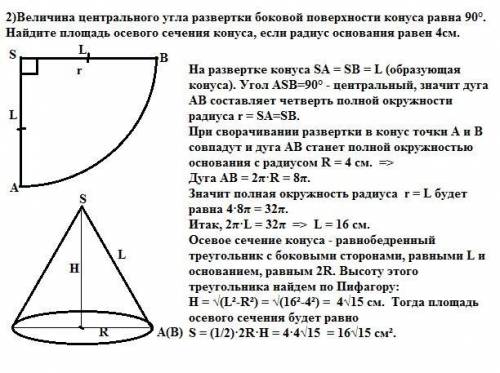
2) На развертке конуса SA = SB = L (образующая конуса). Угол ASB=90° - центральный, значит дуга АВ составляет четверть полной окружности радиуса r = SA=SB.
При сворачивании развертки в конус точки А и В совпадут и дуга АВ станет полной окружностью основания с радиусом R = 4 cм. =>
Дуга АВ = 2π·R = 8π.
Значит полная окружность радиуса r = L будет равна 4·8π = 32π.
Итак, 2π·L = 32π => L = 16 см.
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами, равными L и основанием, равным 2R. Высоту этого треугольника найдем по Пифагору:
H = √(L²-R²) = √(16²-4²) = 4√15 см. Тогда площадь осевого сечения будет равна
S = (1/2)·2R·Н = 4·4√15 = 16√15 см².
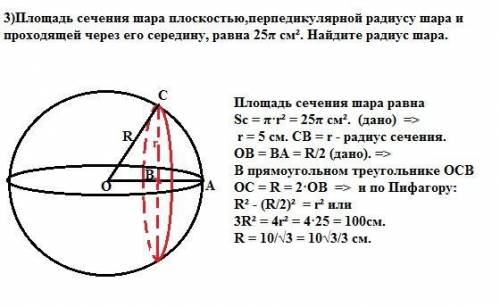
3) Площадь сечения шара равна
Sc = π·r² = 25π см². (дано) =>
r = 5 см. CB = r - радиус сечения.
ОВ = ВА = R/2 (дано). =>
В прямоугольном треугольнике ОСВ ОС = R = 2·ОВ => и по Пифагору:
R² - (R/2)² = r² или
3R² = 4r² = 4·25 = 100см.
R = 10/√3 = 10√3/3 см.

∠NBC = 60°
∠ABN = 90° - ∠NBC = 30°
AB = BN, значит ΔABN равнобедренный, углы при основании равны:
∠BAN = ∠BNA = (180° - 30°)/2 = 75°
∠NAD = 90° - ∠BAN = 90° - 75° = 15°
2. ∠BAF = ∠DAF так как AF - биссектриса,
∠DAF = ∠BFA как накрест лежащие при пересечении AD║BC секущей AF, ⇒ ∠BAF = ∠BFA, треугольник BAF равнобедренный,
АВ = BF = 2 см
∠CFE = ∠AFB как вертикальные
∠CEF = ∠BAF как накрест лежащие при пересечении AB║CD секущей АЕ,
∠AFB = ∠BAF как доказано выше, ⇒
∠CFE = ∠CEF, ⇒ треугольник CFE равнобедренный,
CF = CE = 3 см
АВ = 2 см
ВС = 2 + 3 = 5 см
Pabcd = (AB + BC)·2 = (2 + 5)·2 = 14 см
3. В треугольнике АВЕ АВ = 5 см, АЕ = 3 см, ВЕ = 4 см, значит это прямоугольный (египетский) треугольник, значит ВЕ - высота трапеции.
ЕВСК - прямоугольник (ВЕ = СК как высоты трапеции, ВЕ║СК как перпендикуляры к одной прямой), ⇒ ЕК = ВС = 6 см.
ВС = 6 см
AD = 3 + 6 + 1 = 10 см
Sabcd = (AD + BC)/2 · BE = (10 + 6)/2 · 4 = 32 см²