Внимание : тут два варианта .
62 или 58 см
Объяснение:
Вариант 1 (если бисс АК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг АВК–равнобед =>АВ=ВК=11 и =СD (как стороны парал);
2) ВС=11+9=20=АD;
3) Р =( 11+20)*2=62 см
Вариант 2 (если бисс DК)
1) уг 1=уг 2 (как накрест лежащие при парал прямых);
уг 1=уг 3 (тк бисс);
тогда уг 2=уг3 => треуг DСК–равнобед =>DС=СК=9 и =АВ (как стороны парал);
2) ВС=11+9=26=АD;
3) Р =( 9+20)*2=58
Чертёж в приложении.
Если что-то непонятно , пишите в комментах.
Успехов в учёбе! justDavid
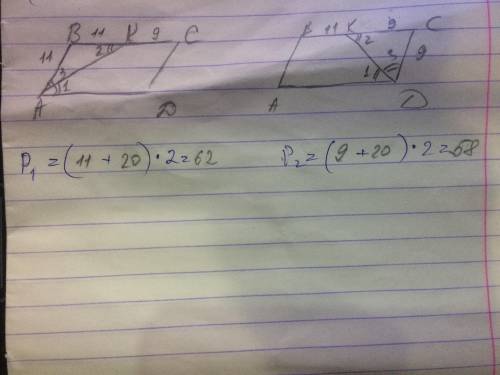
Треугольник АВС с координатами вершин A(4;2; 1), B(0;-6;2),C(0;-2;-6) является равнобедренным, так как АВ = АС = 9 см
Объяснение:
1) Найдём длину стороны АВ, для чего вычислим расстояние между точками A (4; 2; 1) и B (0; -6; 2) :
d = √[(xb - xa)^2 + (yb - ya)^2 + (zb - za)^2] =
= √[(0 - 4)^2 + (-6 - 2)^2 + (2 - 1)^2] =
= √[(-4)^2 + (-8)^2 + 1^2] = √(16 + 64 + 1) = √81 = 9.
Таким образом, длина стороны АВ = 9 см.
2) Найдём длину стороны ВС, для чего вычислим расстояние между точками В (0; -6; 2) и С (0; -2; -6) :
d = √[(xc - xb)^2 + (yc - yb)^2 + (zc - zb)^2] =
= √[(0 - 0)^2 + (-2 - (-6))^2 + (-6 - 2)^2] =
= √(0^2 + 4^2 + (-8)^2) = √(0 + 16 + 64) = √80 ≈ 8,944
Таким образом, длина стороны ВС ≈ 8,944 см
3) Найдём длину стороны АС, для чего вычислим расстояние между точками A (4; 2; 1) и С (0; -2; -6) :
d = √[(xc - xa)^ 2 + (yc - ya)^2 + (zc - za)^2] =
= √[(0 - 4)^2 + (-2 - 2)^2 + (-6 - 1)^2] =
= √[(-4)^2 + (-4)^2 + (-7)^2] = √(16 + 16 + 49) = √81 = 9.
Таким образом, длина стороны АС = 9 см
4) Как следует из выполненных расчетов, в треугольнике АВС, заданного координатами своих вершин A(4;2; 1), B(0;-6;2),C(0;-2;-6),
длина стороны АВ равна длине стороны АС, в силу чего данный треугольник является равнобедренным:
ответ: Треугольник АВС с координатами вершин A(4;2; 1), B(0;-6;2),C(0;-2;-6) является равнобедренным, так как АВ = АС = 9 см