Присвоим точкам обозначения: A, B, C.
На трех точках A, B, C, не принадлежащих одной прямой, можно построить только одну плоскость .
Отрезки, которые соединяют точки, имеют по две точки, которые принадлежат одной плоскости: АВ, ВС, СА.
Если две точки прямой принадлежат плоскости, то и все остальные точки на этой прямой принадлежат плоскости. Следовательно, любая точка на отрезках АВ, ВС, СА принадлежит плоскости.
Любая прямая, пересекающая два отрезка на плоскости, имеет с ними две точки пересечения, которые принадлежат плоскости. Следовательно, и все остальные точки любой прямой, пересекающей два отрезка, лежат в плоскости точек А, В, С.
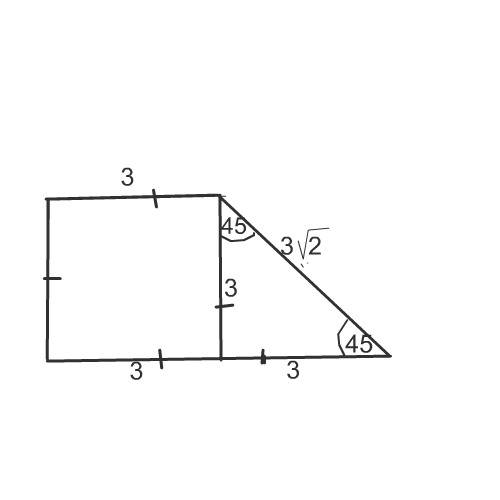
Сделаем рисунок к задаче.
Высота этой трапеции отсекает от нее прямоугольный равнобедренный треугольник с гипотенузой 3√2.
Такой треугольник - половина квадрата с диагональю=гипотенузе.
Формула диагонали квадрата ( формула гипотенузы равнобедренного прямоугольного тр-ка).
d=а√2, где а- сторона квадрата, а в равнобедренном прямоугольном треугольнике - катет. Знание этой формулы часто избавляет от лишних вычислений.
d=СК
СК =3√2=СН√2
СН√2=3√2
СН=3 см
СН=НК как равный катет.
АК=2НК
ВС=АК:2
Площадь трапеции равна Н*(АВ+ВС)
S=3*(3+6):2=13,5 см²
кут АВО=16 градусів, кут DAB=16 градусів, кут ВОА=178градусів
Объяснение:
Дано: коло з центром О; ОА і ОВ радіуси, кут АВО=16градусів
Знайти: кути трикутника ОАВ
розв*язання: так як ОА=ОВ, то кут ОВА=ОАВ=16градусів. Тоді кут ВOA=180градусі - (16+16)=178градусів