Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою 
і проекцією цього катета на гіпотенузу:
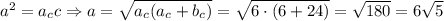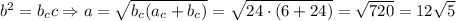см
см
Площа 
прямокутного трикутника знаходится як півдобуток його катетів:
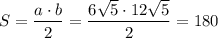см²
Другий б
Висота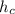 
прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
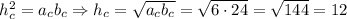см
Площа 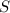будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти 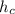, що до неї проведена:
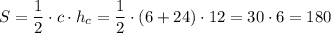см²
Відповідь: 180 см².
mn - средняя линия
ab=cd=8
bc=6
mn = (bc+ad) / 2
уг. авс=уг. всd=120
уг. bad = уг. cda = 360-120-120=60
проведем высоту вн
рассмотри треугольник анв - прямоугольный
уг. в = 90-уг. = а=90-60=30
ан=0,5*ав=0,5*8=4 (свойство угла в 30 градусов в прямоугольном треугольнике)
проведем высоту cl
рассмотри треугольник cld - прямоугольный
уг. c = 90-уг. = d=90-60=30
dl=0,5*cd=0,5*8=4 (свойство угла в 30 градусов в прямоугольном треугольнике)
ad=ah+hl+ld
hl=bc=6
ad=4+6+4=14
mn = (6+14) / 2=20/0=10