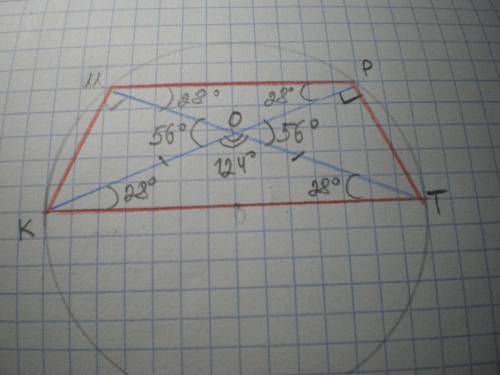
118°, 118°, 62°, 62°
Объяснение:
Дано: КМРТ - трапеция, МК=РТ, КТ=D (окружности), КР и МТ - диагонали, ∠РОТ=∠МОК=56°. Найти ∠К, ∠М, ∠Р, ∠Т.
Решение: ΔКМТ=ΔТРК, т.к. КР=МТ как диагонали равнобедренной трапеции, КМ = РТ по условию, сторона КТ - общая. Значит, ∠ОКТ=∠КТО.
∠КОТ=180-56=124°; ∠ОКТ=∠КТО=(180-124):2=28°.
ΔМОР; ∠МРО=∠ОМР=∠ОКТ=∠КТО=28° как внутренние накрест лежащие при МР║КТ и секущих МТ и КР.
∠КМТ=∠КРТ=90° как углы, опирающиеся на диаметр окружности.
∠М=∠Р=90+28=118°
∠К=∠Т=180-118=62° по свойству углов трапеции, прилежащих к боковой стороне
1)Пусть векторы имеют соответственно координаты: а(х1;у1) ; b(х2;у2),тогда
х1+х2=2 у1+у2=1
х1-х2=-4 у1-у2=3
2*х1=-2 2*у1 =4
х1=-1 у1 =2
х2=3 у2=-1
Таким образом а(-1;2) ; b(3;-1).
2) Разложим вектор с=m*a+k*b , где m и k- постоянные числа, тогда
х3= m*x1+k*x2 y3= m*y1+k*y2
10 = -1m+3k I *2 Умножим на 2 и сложим совторым ур-ем
-5 = 2m-1k
15 = 5k , k=3, тогда m=-1
Таким образом с=-1*a+3*b .
3) сos(a,b)=(x1*x2+y1*y2)/(корень из (х1^2+y1^2))* (корень из (х2^2+y2^2))=
= (-1*3+2*(-1))/ (корень из ((-1)^2+2^2))* (корень из (3^2+(-1)^2)) =
=-5/ корень из 5*корень из10 =-1/корень из2,
Значит угол между векторами 135 градусов.