Объяснение:
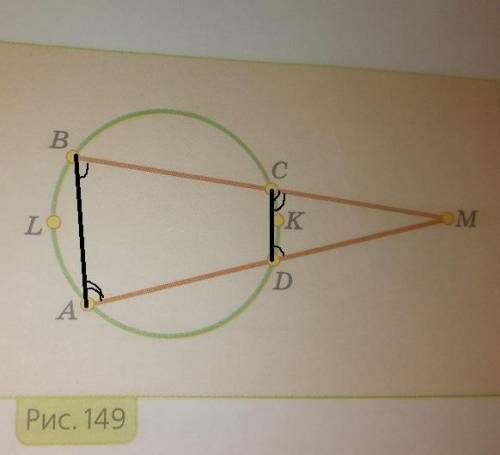
Соединим А и В, С и D. Четырехугольник ABCD - вписанный, значит <ABC+<ADC=180° и <CDM+<ADC=180°, значит <ABC=<CDM. Аналогично <BAD=<DCM.
Из тр-ка △CMD <CMD(AMB)=180-<CDM-<DCM=180-<ABC-<BAD
<ABC=1/2*(AD+CD); <BAD=1/2(BC+CD).
<AMB=180-1/2*(AD+CD)-1/2*(BC+CD)=180-1/2*(AD+CD+BC)-1/2*CD
Для дуг окружности можно записать:
AD+CD+BC=360-AB - подставим в последнее выражение:
<AMB=180-1/2*(360-АВ)-1/2*СD=180-180+1/2*АВ-1/2*СD=1/2*(AB-CD)=1/2*(ALB-CKD)
2) сторона ромба равна меньшей диагонали, значит, углы в этом ромбе:60, 120,60 и 120градусов. треугольникАВС, образованный меньшей диагональю и сторонами ромба, равносторонний. его площадь равна 0,5·4·4·√3:2=4√3, площадь треугольника АОВ=0,5 площади АВС, т.е. 2√3. С другой стороны, площадь треугольника АОВ=0,5·4· r.=2r. Тогда r=√3, а площадь вписаннонго круга = π· r² =3π