Пусть ABCD - равнобокая трапеция с основаниями BC u AD, AB=CD - боковые стороны трапеции. Угол BAD = углу CDA = 60° BE= H = 6√3 (cм) - высота трапеции.
В трапецию можно вписать окружность в том случае, если суммы её противоположных сторон равны ⇒ BC + AD = AB + CD = 2*AB Площадь трапеции равна произведению полусуммы ее оснований на высоту трапеции. S = (BC + AD)/2 * H S = 2*AB / 2 * BE S = AB * 6√3
В прямоугольном треугольнике ABE: AB - гипотенуза, BE u AE - катеты. Угол BAE = 60° AB = BE / sin60° AB = 6√3 / √3/2 = 12 (cм)
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть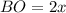
см и 
см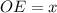, тогда 
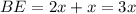, что по условию он равен 9 см.
Следовательно,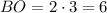
см и 
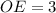см
Аналогично, пусть теперь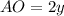
см и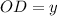 
, тогда 
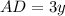и по условию равен 12 см
Таким образом,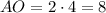
см и 
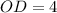см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника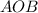
По теореме Пифагора из прямоугольного треугольника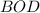
Тогда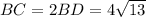
см
Из прямоугольного треугольника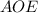
по теореме Пифагора
Тогда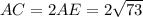
см
ответ:
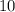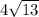см;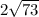 
см; 
см.