Объем конуса находят по формуле: V = 1/3 · Sосн · H, где Sосн - площадь основания, H - высота. В основании - круг, Sосн = πR², где R - радиус основания.
Пусть дан конус (см. рис.) . SО - высота, SВ - образующая, ОВ - радиус. По условию SО : SВ = 4 : 5 и V = 96π см³.
ΔSОВ - прямоугольный. Если принять, что SО = (4х) см, SВ = (5х) см, то по теореме Пифагора ОВ² = SВ² - SО² = (5х)² - (4х)² = 25х² - 16х² = 9х², откуда, учитывая, что длины сторон положительны, ОВ = 3х (см).
Подставляем полученные выражения в формулу объема:
V = 1/3 · πR² · H = 1/3 · π · ОВ² · SО = 1/3 · π · (3х)² · 4х = 12πх³ = 96π, т.е.
12πх³ = 96π,
х³ = 8,
х = 2.
Тогда ОВ = 3 · 2 = 6 (см), SB = 5 · 2 = 10 (см).
Площадь полной поверхности конуса равна:
Sполн = Sосн + Sбок = πR² + πRL = πR(R + L), где R - радиус основания, L - образующая конуса.
Значит, Sполн = π · ОВ · (ОВ + SВ) = π · 6 · (6 + 10) = 6π · 16 = 96π (см²).
ответ: 96 см².

10 см
Объяснение:
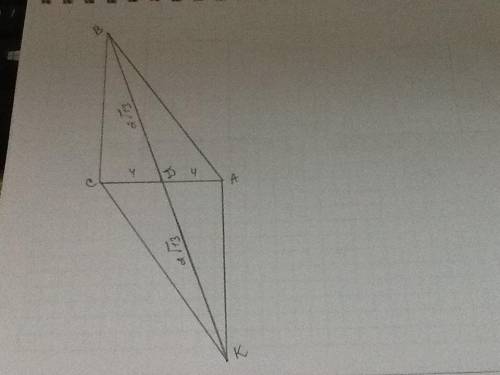
Дано: ΔАВС - прямоугольный, ∠С=90°, ВD - медиана, BD=2√13 cм, АС=8 см. АВ - ?
Если в условии дана медиана треугольника, я решаю задачу, достроив треугольник до параллелограмма. Теорема об удвоении медианы:
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Продлеваем медиану на такую же длину и строим параллелограмм АВСК, где диагональ АС=8 см, диагональ ВК=2√13+2√13=4√13 см.
Тогда АС²+ВК²=2(АВ²+ВС²).
208+64=2(АВ²+ВС²)
272=2(АВ²+ВС²)
АВ²+ВС²=136.
Вернемся к ΔАВС. По теореме Пифагора
АВ²+ВС²=136
АВ²-ВС²=64 (т.е. АС²)
2АВ² = 200; АВ²=100; АВ=10 см.
5см 100% правильно
Объяснение:
потому что дотична дотикається до кола и радуис ровняеться 5см тогда и расстояние равняеться 5см