Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельные прямые. Следовательно нам надо найти в плоскости ADB прямую параллельную DB и проходящую через точку E.
Следовательно это будет прямая содержащая отрезок EF - среднюю линию ΔADB.
Повторив эти рассуждения для плоскостей ABC и ADC, получим, что сечением будет ΔEFG образованный средними линиями EF, FG и GE треугольников ADB, ADC и ABC соответственно.
В каждом из треугольников мы знаем сторону основания, соответственно можем найти средние линии:
EF = FG = 7.5
FG = 9
Найдем площадь треугольника EFG, найдя высоту FH проведенную к основанию EG равнобедренного трегольника EFG
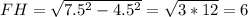
Теперь найдем и площадь сечения по формуле полупроизведения высоты на основание:
S = 6 * 9 / 2 = 27
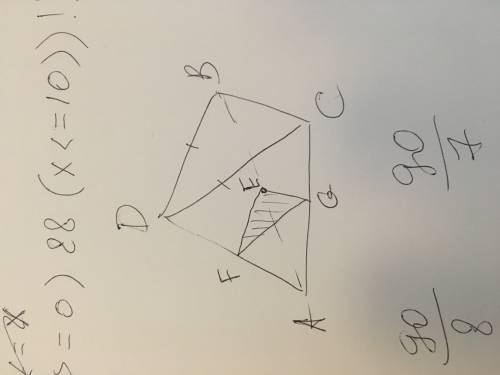
приложение №1):
Через точку С проводим диаметр окружности. Обозначаем его СМ. Проводим отрезок АМ. В треугольнике АМС угол А прямой (МС диаметр вписанного прямоугольного треугольника). АВДМ - трапеция (АМ||ВД), углы АВМ и АДМ равны (опираются на одну хорду АМ). Трапеция АВДМ - равнобедренная, АВ=МД=3 см.
Треугольник МСД прямоугольный. МД=3 см, ДС=4 см, МС=√(3³+4³)=5 см.
Радиус 5/2=2,5 см.
приложение №2):
Радиус описанной окружности вокруг четырехугольника, равен радиусу описанной окружности любого треугольника, образованного сторонами этого четырехугольника.
Радиус описанной окружности -
R=a/2sinα , где а - сторона треугольника, α - противолежащий угол.
Рассматриваем треугольник НВС, где Н точка пресечения диагоналей.
Прямоугольный, угол Н (по условию), угол В - β, угол С - (90-β).
R=СД/2sinβ=2/sinβ;
R=АВ/2sin(90-β)=3/2cosβ.
Делим одно выражение на другое.
3/2cosβ * sinβ/2=3tgβ/4=1, tgβ=4/3
R=2/sin(atgβ)=2.499999=2.5 см.