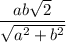1)в равнобедренном треугольнике углы при основании равны поэтому каждый угол равен (180-146):2=17градусов
2)внешний угол треугольника равен сумме внутренних углов не смежных с ним, поэтому внешний угол при вершине А = угол В+угол С=29+65=94градуса.
3)внешний угол треугольника равен сумме внутренних углов не смежных с ним, поэтому 90+39=129градусов-внешний угол при вершине другого острого угла
4)у ромба сумма острого и тупого угла равна 180 градусов, поэтому острый угол равен 180-136=44 градуса
5)Пусть хорда АВ-диаметр окружности, тогда вписанный угол АСВ-прямой, то есть равен 90 градусов. По условию угол между хордами 48 градусов. Тогда в прямоугольном треугольнике АВС угол В=90-48=42градуса. Вписанный угол равен половине дуги на которую он опирается. Против угла 42 градуса лежит дуга 42*2=84 градуса.
Пусть дан треугольник АВС с прямым углом А, в котором проведена биссектриса АЕ, длину которой нужно найти.
Биссектриса треугольника делит сторону треугольника на отрезки, пропорциональные прилежащим сторонам.
Запишем пропорцию:
Пусть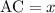 . Тогда
. Тогда 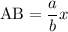 .
.
Запишем теорему Пифагора для треугольника АВС:
Значит:
Запишем теорему синусов для треугольника АЕС:
Так как АЕ - биссектриса, то ЕАВ и ЕАС равны по половине прямого угла, то есть по 45°.
Синус угла С определим как отношение противолежащего катета к гипотенузе:
Теперь можем найти биссектрису:
ответ: