--- 1 ---
из точки А проводим вправо отрезок длиной а к точке В
Здесь а должно быть > 25 с тем, чтобы АВ было большим основанием трапеции
от точки В влево откладываем отрезок 50 и из точки Q строим окружность радиусом 48, пересечение этой окружности с верхним основанием даст точку трапеции Д
Расстояние QB = 50, это гипотенуза
Расстояние QД = 48, это катет.
Катет ВД по Пифагору
ВД = √(50²-48²) = √(2500 - 2304) = √196 = 14 см
Площадь треугольника QВД через катеты
S = 1/2*QД*ВД = 1/2*48*14 = 24*14 = 336
Площадь треугольника QВД через гипотенузу и высоту к ней
S = 1/2*QВ*ДН = 1/2*50*ДН = 336
25*ДН = 336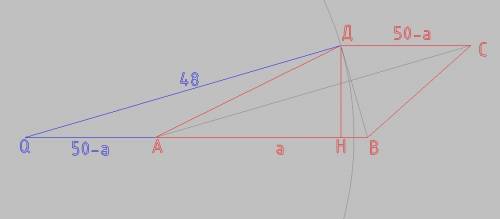
Р = 27 см.
Объяснение:
Так как треугольник равнобедренный, то две его стороны (боковые) равны. В условии не сказано, какая из двух данных нам разных по длине сторон боковая. Следовательно, мы должны проверить два варианта решения.
Первый вариант: пусть основание равно 11 см. Тогда боковые стороны равны по 5 см. Но это противоречит теореме о неравенстве треугольника, по которой большая из трех сторон треугольника должна быть меньше суммы двух других сторон: 11 > (5+5). Значит этот вариант решения не удовлетворяет условию существования треугольника.
Второй вариант: пусть основание равно 5 см. Тогда боковые стороны равны по 11 см. => 11 < (11+5) => условие существования треугольника выполняется. Следовательно, такой треугольник существует и его периметр (сумма всех сторон) равен Р = 11+11+5 = 27 см.