Question

Мені серйозно дуже потрібно! Дякую якщо шо :)
У прямокутний трикутник з кутом 30 градусів вписано коло яке дотикається до сторін трикутника а точках M P та E. Знайдіть кути трикутника МРЕ.​

Answer 1

45, 60, 75

Объяснение:

пусть треугольник МРЕ назовем внутренним, остальные з треугольника- внешними. Каждый из внешних треугольников является равнобедренным с известным углом при вершине, соответственно 90, 60 и 30 градусов. Найдем у этих треугольников углы при основании

(180-30):2=75

(180-60):6075

(180-90):2=45, тогда можно найти каждый угол внутреннего треугольника

180-(75+60)=45

180-(75+45)=60

180-(45+60)=75

Answer 2

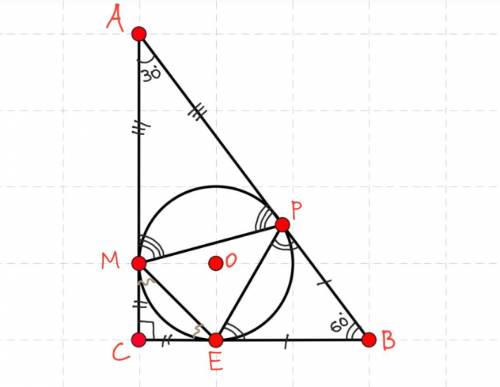
Дано: ΔABC — прямокутний (∠С=90°), ∠А=30°; коло, впис. у ΔABC; М, Р, Е — точки дотику,.

Знайти: ∠ЕМР, ∠МРЕ, ∠РЕМ.

Розв'язання.

Знайдемо третій кут прямокутного трикутника АВС. ∠В= 180°–∠С–∠А= 180°–90°–30°= 60°. (Сума кутів трикутника складає 180°)

1)Існує така властивість: відрізки, проведені з однієї вершини до точок дотику з колом, рівні.

Звідси, АМ=АР, РВ=ВЕ, ЕС=СМ. Це означає, що трикутники МАР, РВЕ і ЕСМ є рівнобедреними.

2) Розглянемо ΔМАР:

АМ=АР => ∠АМР=∠АРМ= (180°–∠А):2= (180°–30°):2= 150°:2= 75°.

3) У ΔРВЕ: ∠В= 60°, РВ=ВЕ => ∠ВРЕ=∠ВЕР= (180°–∠В):2= (180°–60°):2= 60°.

4) У ΔЕСМ: ∠С= 90°, ЕС=СМ => ∠СЕМ=∠СМЕ= (180°–90°):2= 90°:2= 45°.

5) Тепер ми можемо знайти всі кути трикутника МРЕ.

∠ЕМР= 180°–∠СМЕ–∠АМР= 180°–45°–75°= 60°.

∠МРЕ= 180°– ∠АРМ–∠ЕРВ= 180°–75°–60°= 45°.

∠РЕМ= 180°–∠ВЕР–∠СЕМ= 180°–60°–45°= 75°.

Відповідь: 45°, 60°, 75°.