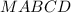 - правильная четырехугольная пирамида, около которой описан конус
- правильная четырехугольная пирамида, около которой описан конус 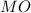 ⊥
⊥ 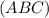
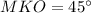
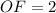 см
см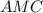 - осевое сечение конуса, где
- осевое сечение конуса, где 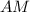 и
и 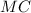 - образующие конуса
- образующие конуса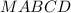 - правильная четырехугольная пирамида,
- правильная четырехугольная пирамида, 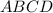
 ∩
∩ 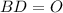
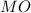 ⊥
⊥ 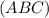
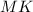 ⊥
⊥ 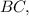 тогда
тогда 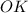 ⊥
⊥ 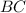 и
и  как линейный угол двугранного угла
как линейный угол двугранного угла  - центр окружности, описанной около квадрата
- центр окружности, описанной около квадрата  , т. е.
, т. е. 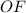 ⊥
⊥ 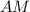
 тогда
тогда 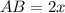
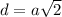 , где
, где 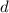 - диагональ квадрата,
- диагональ квадрата,  - сторона квадрата
- сторона квадрата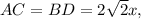 ( как диагонали квадрата)
( как диагонали квадрата)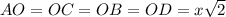
 - прямоугольный, равнобедренный, следовательно
- прямоугольный, равнобедренный, следовательно 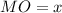
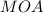 - прямоугольный
- прямоугольный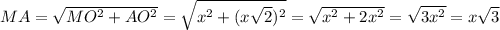
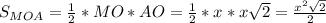 ,
,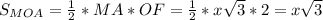
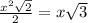
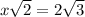
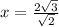
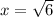
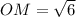 см
см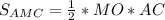
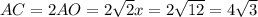 см
см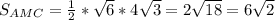 (см ²)
(см ²)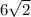 см²
см²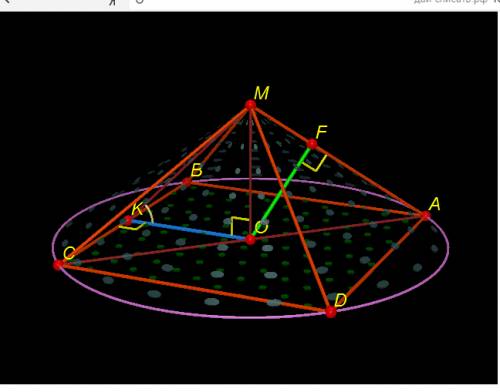
1) находим гипотенузу за теоремой пифагора, AB=25.
есть формула нахождения высоты за тремя сторонами: Ha=2корень(p(p-a)(p-b)(p-c))/a
p=(a+b+c)/2
подставив в эту формулу данные, находим высоту 12, она есть диаметром, значит r=12/2=6
длина окружности=2пr=12п
2)Sквадрата=a^2 a=корень из S
r вписанной окружности для квадрата = a/2
r=S^2/2 длина=2пr=S^2п
нарисуй квадрат и вписанный в него круг, точками касания будут середины сторон квадрата, берем те, которые на соседних сторонах и отмечаем эту дугу. угол, на которую она опирается - прямой. это видно по рисунку
90*=п/2 длина дуги=r*альфа=S^2/2*п/2=пS^2/4
площадь вне окружности можно найти отняв от площади квадрата площадь окружности. Sокружности=пr^2=(S^4п)/4 S вне окружности=S-(S^4п)/4