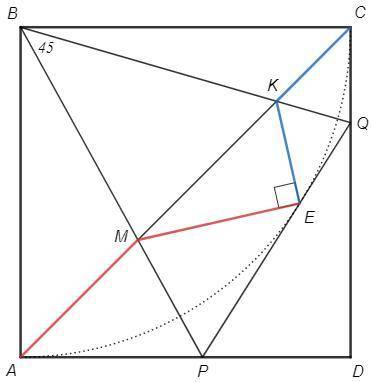
Продлим BM и BK до пересечения со сторонами квадрата в точках P и Q. Рассмотрим треугольник PDQ.
Центр вневписанной окружности треугольника - пересечение биссектрис одного внутреннего и двух внешних углов.
Центр вневписанной окружности лежит на биссектрисе угла D. Отрезок PQ виден из центра вневписанной окружности под углом 90 -D/2. Точка B обладает обоими свойствами, следовательно является центром вневписанной окружности треугольника PDQ.
Пусть E - точка касания вневписанной окружности.
A, C - также точки касания (радиус в точку касания перпендикулярен касательной)
PA=PE, QC=QE (отрезки касательных из одной точки)
PB, QB - биссектрисы
△APM=△EPM, △CQK=△EQK (по двум сторонам и углу между ними)
Следовательно AM=EM, CK=EK
∠MAP=∠MEP=45, ∠KCQ=∠KEQ=45 => ∠MEK=90
27
Объяснение:
проведём высоту ВН. уг. НВС=90°=>уг. АВН=60°. уг. АНВ=90°. АН=АД-ВС=10см. ВН =√АВ^2-АН^2= √26^2-10^2=√576=24 см
площадь =(30+24):2=27 см