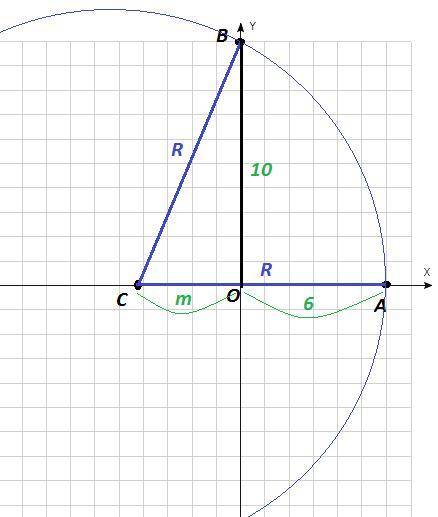
Координаты точки на оси Ox : A (6;0)
Координаты точки на оси Oy : B (0;10)
Так как 6<10, значит, центр окружности лежит слева от оси Oy.
Координаты центра окружности на оси Ox : С(-m;0)
R = CA = m + 6
ΔBOC , R = CB, теорема Пифагора :
R² = m² + 10²
(m + 6)² = m² + 10²
m² + 12m + 36 = m² + 100
12m = 64; 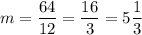
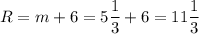
Общее уравнение окружности с центром в точке С и радиусом R
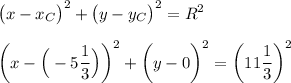
Так как абсцисса центра окружности отрицательная, то в первой скобке должен быть знак плюс.
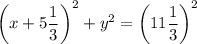
Если подгонять ответ под схему в условии, то знак минус придётся убрать в числитель дроби :
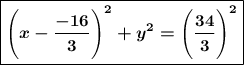
AC = AD; AB = AE; CE = 7 (сантиметров); AE = 3 (сантиметра).
Найти:AB; BD.
Доказать:△ ACE = △ ABD.
Доказательство:По данным условиям можно сделать вывод, что задачу возможно доказать по 1 признаку равенства треугольников.
1 треугольник = 2 треугольник
2 стороны = 2 стороны
угол между 2 сторонами = угол между 2 сторонами
AB = AE (по условию); AC = AD (по условию).
∠ A - общий, поэтому является равным в обоих треугольниках.
⇒ △ ACE = △ ABD (по 1 признаку равенства треугольников)
ч.т.д.
Решение:Из "Доказательство" ⇒ BD = CE = 7 (сантиметров); AB = AE = 3 (сантиметра). (т.к. треугольники равны)
ответ: 7 сантиметров; 3 сантиметра.