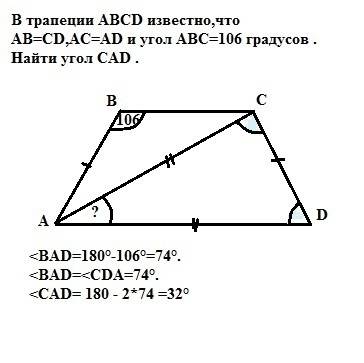
Втрапеции авсd диагонали пересекаются в точке е. площадь треугольника аве равна 72, площадь треугольника сdе равна 50. найти площадь трапеции авсd.

👇

Ответ:

myshkin02

19.03.2021

Треугольники АВЕ и CDE подобны по двум углам при основании. Поскольку площади подобных треугольников относятся как квадраты соответствующих сторон, то ВЕ2 : DЕ2 = 72 : 50, откуда ВЕ : DЕ = 6 : 5. Так как в треугольниках ВСЕ и DCE стороны ВЕ и DE лежат на одной прямой и вершина С, то их площади относятся как основания,

т.е. SBCE : SDCE = BE : DE = 6 : 5. Откуда SBCE = 6 : 5 50 = 60.

Таким образом, площадь трапеции ABCD равна

SABCD = 72 + 50 + 60 + 60 = 242.

4,7(40 оценок)

Открыть все ответы

Ответ:

elviraborysenko

19.03.2021

Решать в общем виду долго и скучно. Но если условие корректное (то есть не зависит от не заданного соотношения сторон AB и AC), то можно рассмотреть частный случай, а именно равнобедренный треугольник ABC. Если взять за x длину боковой стороны (AB или AC), то основание BC будет равно x*корень(3). То есть периметр x+x+x*корень(3) = 10 и боковая сторона равна: x = 10/(2+корень(3)). Расстояние до центра описанной в условии окружности находим из треугольника ANO, где N - точка касания окружностью луча AB. Не трудно показать, то AN = x*(1+корень(3)/2) = 10*(1+корень(3)/2)/(2+корень(3)) = 5. А гипотенуза AO имеет длину 5/sin(60) = 10.

Можно также рассмотреть треугольник ABC с длиной стороны AC стремящейся к нулю. Не трудно показать, что в этом случае описанная в условии окружность должна касаться линии AB вблизи стремящейся к нулю окрестности точки B, длина AB будет равна 10/2 = 5, а угол между AB и направлением на центр искомой окружности равен 60 (половине 120 - центр будет лежать на биссектрисе к углу A). То есть имеем прямоугольный треугольник ABO (угол B - прямой) с углом A = 60 градусов и катетом AB = 5. AO = 5/sin(60) = 10.

4,6(18 оценок)

Ответ:

PashaPlaytri

19.03.2021

В трапеции АВСD углы, прилежащие к боковой стороне, в сумме равны 180° (как односторонние при параллельных прямых ВС и АD и секущих - боковых сторонах АВ и СD). =>

<BAD = 180° - 106° = 74°.

Так как АВ=СD - трапеция равнобедренная, то углы при основаниях равны => <BAD=<CDA = 74°.

Так как AC=AD (дано) => треугольник DAC равнобедренный и углы при основании CD равны. <ACD=<CDA = 74°.

Тогда угол при вершине треугольника САD равен 180-2*74= 32° (так как сумма внутренних углов треугольника равна 180°)

ответ: угол САD=32°.