Объяснение:
1. 3) (неравенство треугольника);
2. Т.к. CD можно рассматривать как секущую к прямым BC и AD, то доказательство параллельности AD и BC сводится к нахождению каких-нибудь особых пар углов, которые при параллельности прямых дают определенное значение. Например, можно сказать, что т.к. угол ADC = 15° + 75° = 90°, а угол BCD равен также 90°, то сумма BCD и ADC равна 180. Эта пара углов называется внутренние односторонние. Доказывается, что если их сумма равна 180° (как в нашем случае), то прямые, которые пересекаются секущей, параллельны. То есть AD║BC.
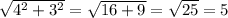. Значит, сторона ромба равна 5 см (в ромбе все стороны равны).
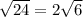см.
Объяснение:
Дано:
CD=AB
O-центр окр
A,B,C,D∈окр
CD=17см
CO=15 см
Найти P(AOB)
Для начала найдет стороны треугольника AOB, для этого совету вспомнить,что O-центр окружности, а A,B,C,D точки лежащие на окружности, значит расстояние от O до любой из этих точек - радиус, получается, что AO=BO=CO=DO=15см, по условию, CD=AB=17см. Периметр - это сумма всех стороны, значит P(AOB)=47см, Сейчас всё оформлю
Пусть ΔAOB - равнобедренный, так как AO=BO=CO=DO как радиусы окружности ⇒
AO=BO=15 см,
AB=CD по условию,⇒ AB=17см⇒
PΔAOB=AO+BO+AB=15+15+17=47см
ответ:47см