Question

60 в треугольнике abc биссектрисы, проведенные из вершин b и с пересекаются в точке o. прямая, проведенная через точку о, параллельно ab пересекает bc в точке e, а прямая, проведенная через точку ooo, параллельно ас пересекает вс в точке ddd. найдите длину od, если oe=14,ed=16,bc=40

Answer 1

угол АСО = угол DCO, угол АСО = угол DOC - как накрест лежащие углы при KD || AC и секущей ОС. Значит, угол DCO = угол DOC => тр.DOC - равнобедренный, OD = DC.Аналогично, тр. ВЕО - равнобедренный, ВЕ = ЕО = 14DC = OD = BC - BE - ED = 40 - 14 - 16 = 40 - 30 = 10

ОТВЕТ: 10

Answer 2

Объяснение:

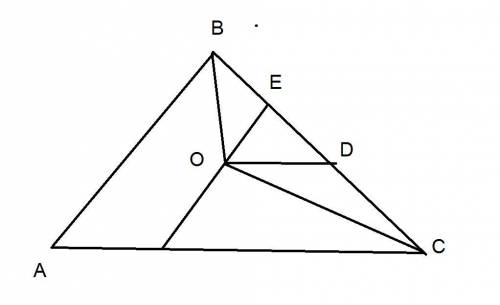
рассмотрим угол B

так как ВО - биссектриса  <АВО=<OВE

так как ОЕIIAB ⇒ <АВО=<BOE (внутренние накрест лежащие углы)

⇒<OВE=<BOE ⇒ ΔOВE - равнобедренный ⇒ BE=EO (1)

такие же рассуждения проведем для  угла С

рассмотрим угол С

так как СО - биссектриса  <DСО=<AСO

так как ОDIIAC ⇒ <DOC=<ACO (внутренние накрест лежащие углы)

⇒<DOC=<DCO ⇒ ΔDOC - равнобедренный ⇒ DO=DC (2)

(1),(2)⇒ РΔEOD=BC

BE=OE=14; ED=16

OD=DC=BC-BE-ED=40-14-16=10

OD=10