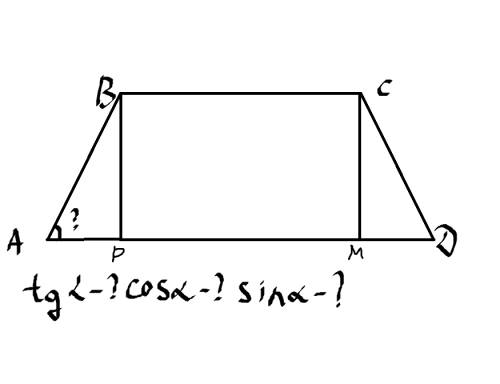
Дано:
AD-BC=8см
AB+CD=10см
sin a-?
cos a-?
tg a-?
Решение
1) Проведем перпиндекуляры из углов B и C к основанию AD
2) Т.к. по условию AD-BC=8 см, то AP+MD+PM-BC=8 см
3) Рассмотрим треугольники ABP и CMD. Они равны по 1 признаку:
1) BP=CM (как перпендикуляры проведенные из равных по величине углов)
2) угол A=D (как углы при основании равнобедренной трапеции)
3) AB=CD (как стороны равнобедренной трапеции)
4) Т.к. треугольники ABP и CMD равны, то AP=MD. Т.к. BC=PM, AP=MD то
AP+MD+PM-BC=8 см
2AP=8 см
AP=4 см
5) AB+CD=10 см - по условию
Т.к. стороны равнобедренной трапеции равны, то
2AB=10 см
AB=5 см, следовательно и CD=5 см
6) Т.к. AB=5 см, AP=4 см, то по теореме Пифагора:
BP=корень (AB^2-AP^2)=корень (25-16)=3 см
7) sin a= BP\AB=3\5=0,6 (синус-отношение противолеж. катета к гипотенузе)
cos a= AP\AB=4\5=0,8 (косинус-отношение прилежащего катета к гипотеннузе)
tg a= BP\AP=0,75 (тангенс-отношение противолеж. катета к прилежащему)
ответ: sin a=0,6 ;cos a=0,8 ;tg a=0,75.
Дано:
AD-BC=8см
AB+CD=10см
sin a-?
cos a-?
tg a-?
Решение
1) Проведем перпиндекуляры из углов B и C к основанию AD
2) Т.к. по условию AD-BC=8 см, то AP+MD+PM-BC=8 см
3) Рассмотрим треугольники ABP и CMD. Они равны по 1 признаку:
1) BP=CM (как перпендикуляры проведенные из равных по величине углов)
2) угол A=D (как углы при основании равнобедренной трапеции)
3) AB=CD (как стороны равнобедренной трапеции)
4) Т.к. треугольники ABP и CMD равны, то AP=MD. Т.к. BC=PM, AP=MD то
AP+MD+PM-BC=8 см
2AP=8 см
AP=4 см
5) AB+CD=10 см - по условию
Т.к. стороны равнобедренной трапеции равны, то
2AB=10 см
AB=5 см, следовательно и CD=5 см
6) Т.к. AB=5 см, AP=4 см, то по теореме Пифагора:
BP=корень (AB^2-AP^2)=корень (25-16)=3 см
7) sin a= BP\AB=3\5=0,6 (синус-отношение противолеж. катета к гипотенузе)
cos a= AP\AB=4\5=0,8 (косинус-отношение прилежащего катета к гипотеннузе)
tg a= BP\AP=0,75 (тангенс-отношение противолеж. катета к прилежащему)
ответ: sin a=0,6 ;cos a=0,8 ;tg a=0,75.

Проанализируем каждое утверждение.
а) Это верно, середина отрезка действительно принадлежит отрезку, но ведь не только середина может принадлежать отрезку (на первом рисунке С - середина отрезка АВ, D - произвольная точка и она тоже лежит на отрезке АВ).
Утверждение а не подходит.
б) Это верно, середина действительно делит отрезок на части. Но ведь не только середина может так делать (обратимся также к первому рисунку, точка D делит отрезок на две части - DB и АD).
Утверждение б не подходит.
в) Это верно. Середина действительно лежит на отрезке и делит его пополам.
Утверждение в подходит.
г) Это верно, середина отрезка действительно равноудалена от концов отрезка. Но ведь не только середина может быть равноудалена от концов отрезка (на втором рисунке изображена точка В, которая равноудалена от концов отрезка АС).
Утверждение г не подходит.
ответ: в).