ответ:6,6,arctg(√5/2)
Объяснение:
На картинке забыл написать чему равен S(BEL).
S(BEL)=(√2×6)/2×(√2/2)=3,
за внимание.
Объяснение:
координаты вектора вычисляются так: из соответствующей координаты конца вектора нужно вычесть соответствующую координату начала вектора.
получим координаты вершин параллелограмма, выраженные через координаты одной точки (точки А, например)
координаты векторов-диагоналей параллелограмма вычисляются аналогично...
косинус угла между векторами = частному от деления скалярного произведения векторов на произведение длин векторов.
скалярное произведение векторов=сумме произведений соответствующих координат.
длина вектора=корню квадратному из суммы квадратов координат (т.Пифагора)
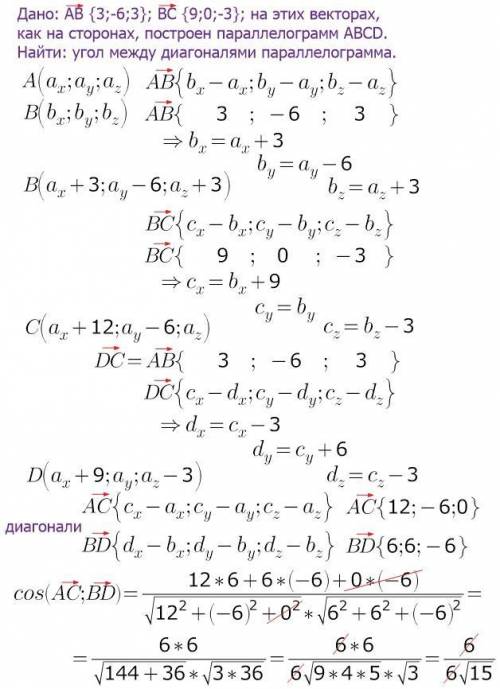
Объяснение:
На РУССКОМ: Причиной смены времён года является наклон земной оси по отношению к плоскости эклиптики и вращение Земли вокруг Солнца. ... Зимой дни становятся короче, а положение Солнца в полдень — ниже, чем в Южном полушарии, где в это время лето. Спустя полгода Земля переходит на противоположную точку своей орбиты.
На Казахском:
Жыл мезгілдерінің ауысуының себебі - жер осінің эклиптика жазықтығына қарай қисаюы және жердің Күнді айналуы. ... Қыста күндер қысқарады, ал күннің түске қарай орналасуы жаз болатын Оңтүстік жарты шардағыдан төмен. Алты айдан кейін Жер өз орбитасының қарама-қарсы нүктесіне ауысады
В сечении получаем четырёхугольник BKLM.
Точки K и M на основании задания расположены на расстоянии 6/2 = 3 ед. от плоскости основания.
Поэтому отрезок KM параллелен основанию.
Точка Р пересечения отрезков KM и BL, лежащих в плоскости сечения, тоже находится на расстоянии 3 ед. от основания.
Проекция отрезка BL на основание - это диагональ BD прямоугольника основания. Треугольники BPF и BLD подобны. Отрезок BF по построению равен (3/4)BD.
Отсюда находим длину отрезка LD.
LD = PF/(3/4) = 3/(3/4) =4 ед.
Получаем первый ответ: BL = √(2² + 4² + 4²) = √36 = 6 ед.
Проведём прямую ВН параллельно KM - это линия пересечения секущей плоскости и плоскости основания пирамиды. Продлим сторону AD до пересечения с ВН.
По свойству полученного параллелограмма ВСАН отрезок АН = ВС = 3 ед. Длина ТН = (2/2) + 3 = 4 ед.
Угол Н равен углу ВСА.
Его синус равен 4/√(2² + 4²) = 4/√20 = 4/(2√5) = 2/√5.
Отсюда находим: TR = TH*sin H = 3* (2/√5) = 6/√5.
Двугранный угол между секущей плоскостью и основанием равен плоскому углу, полученному при пересечении двух плоскостей третьей, проведенной перпендикулярно их линии пересечения. Это угол MRT.
Получаем второй ответ:
∠MRT = arctg MT/TR = arc tg(3/(6√5) arctg (√5/2) =
= arc tg 1,118034 = 0,841 радиан или 48,19 градуса.
Находим длину наклонной MR = √(MT² + TR²) = √(9 + (36/5)) = 9/√5.
Отсюда косинус угла MRT равен:
cos (MRT) = cos φ = TR/MR = (6/√5)/(9/√5) = 2/3.
Теперь определяем площадь проекции сечения на основание как площадь основания минус площади двух треугольников.
So = 2*4 - (1/2)*1*4 - (1/2)*2*2 = 8 - 2 - 2 = 4.
Получаем третий ответ: Sсеч = So/cos φ = 4/(2/3) = 6 кв.ед.