sin (236% - sin (270 ° 34%) - сos34, тут третя чверть, в якій синус негативний, а 270 ° менят функцію на кофункцію, тобто синус на косинус. cos-1306 ° - сos (1306 ° ) в силу парності косинуса cos (+1306 ° - сosl (3 "360 ° -2269можно відкинути три періоди, тобто 3 * 360 °, отримаємо соs (-226% -сos (226% -cos (270 ° 449-- sin44 ° tgl-6219- - tg (6219-- tg (2 * 360 ° -999% 3
12 см.
Объяснение:
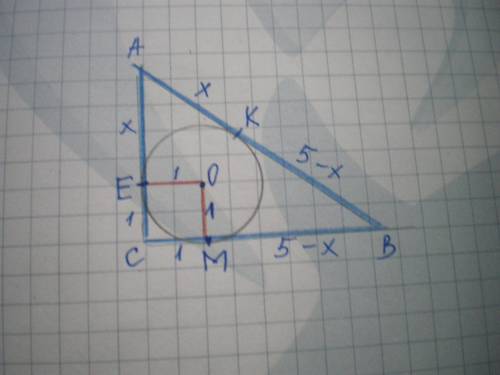
Дано: ΔАВС - прямокутний, ∠С=90°, АВ=5 см, ОЕ-радіус, ОЕ=1 см. Знайти Р(АВС).
Нехай коло торкається гіпотенузи у точці К, катета АС у точці Е, катета ВС у точці М.
Відрізки дотичних, проведених з однієї точки до кола, рівні між собою.
Нехай АК=х см, тоді ВК-5-х см; але АЕ=АК, отже, АЕ=х см.
ВМ=ВК=5-х см.
Дотична до кола перпендикулярна до радіуса, проведеного у точку дотику. Тому СЕ⊥ЕО, ОМ⊥СМ, ЕС⊥СМ, ЕО=ОМ як радіуси, отже ОЕСМ - квадрат, ЕС=СМ=1 см.
АС=х+1 см.
Знайдемо периметр АВС:
Р=АВ+АС+ВС=5+(х+1)+(1+5-х)=5+х+1+1+5-х=12 см.
Классная задача Пусть дан прямоугольный треугольник АСВ, ∠С=90°, по свойству отрезков касательных, проведенных из одной точки к одной окружности. расстояние от этих точек до точек касания одинаковы, если К, Т и Р обозначить точки касания соответственно к гипотенузе АВ, катетем СВ и АС соответственно, то по этому свойству, если обозначить ВТ=х, то и ВК=х, тогда
АК=АВ-ВК=5-х, но тогда и АР=5-х, СТ=СР=1, сложим отрезки, из которых состоят катеты и гипотенуза. АВ=х+5-х=5, СВ=х+1; АС=5-х+1=6-х.
Периметр Р=АВ +СВ+АС=5+(1+х)+(6-х)=12/см/
ответ 12 см
sin (236°)= sin (270°-34°)=-cos34°, здесь третья четверть, в которой синус отрицательный, а 270° менят функцию на кофункцию, т.е. синус на косинус.
cos(-1306°)= cos(1306°) в силу четности косинуса
cos(1306°)= cos(3*360°-226°)можно отбросить три периода, т.е. 3*360°, получим cos(-226°)=cos(226°)=cos(270°- 44°)=- sin44°
tg(-621°)= - tg(621°)=- tg(2*360°-99°)= - tg(-99°)=tg(99°)=tg(90°+9°)=
-сtg9°